2.3 Gränsvärde

<-- Förra avsnitt

Genomgång

Övningar

Nästa avsnitt -->

Lektion 17 Gränsvärde

Gränsvärde av en funktion

Exempel

Funktionen \( y = f(x) = \) \( {10 \over x\,-\,2} \) har följande graf: \( \qquad \)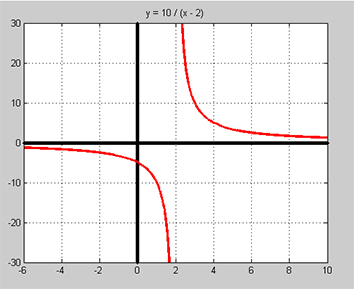

Vad händer med funktionen när \( {\color{White} x} x \to \infty {\color{White} x} \) och \( {\color{White} x} x \to - \infty {\color{White} x} \)?

Vad händer med \( \,y \) när \( {\color{White} x} x \to \infty {\color{White} |}\)?

Som grafen visar närmar sig kurvan \(\, x\)-axeln utan att skära eller ens beröra den. Dvs funktionen går mot \( 0\, \) utan att nå själva värdet \( 0\, \) någon gång. \( f(x)\, \) blir allt mindre ju större \( x \, \) blir. \( \,y \) närmar sig \( 0\, \) när \( x \, \) växer både i positiv och negativ riktning. Kurvan skär aldrig \( \, x \)-axeln. Därför har funktionen inget nollställe.

Funktionsuttrycket bekräftar detta beteende: Täljaren är konstanten \( 10\, \) som aldrig kan bli \( 0\, \). Därför kan hela funktionsuttrycket aldrig bli \( 0\, \). Ett sätt att beskriva detta beteende är:

\[ {10 \over x\,-\,2} \to 0 \quad {\rm när} \quad x \to \infty \qquad {\color{White} x} {\rm vilket\;läses\;så\;här:} {\color{White} x} \qquad {10 \over x\,-\,2} \;\, {\rm går\;mot} \;\, 0 \quad {\rm när} \quad x \;\, {\rm går\;mot} \;\, \infty \]

Det strikt matematiska sättet att uttrycka samma sak är:

\[ \lim_{x \to \infty}\,{10 \over x\,-\,2}\,=\,0 \qquad\qquad\qquad\, {\color{White} x} {\rm vilket\;läses\;så\;här:} {\color{White} x} \quad\; {\color{White} x} {\rm Limes\;\,av} \; {10 \over x\,-\,2} \quad {\rm då} \; x \; {\rm går\;mot} \, \infty \quad {\rm är} \; 0 \, {\rm ,\;vilket\;betyder:} \]

\[ {\color{White} x} {\rm Gränsvärdet\;\,för} \; {10 \over x\,-\,2} \quad {\rm då} \; x \; {\rm går\;mot} \, \infty \quad {\rm är} \; 0 \;{\rm .}\]

Förkortningen  lim  står för det latinska ordet  Limes   som betyder gräns.

Limesbegreppet är centralt i matematiken och kommer att användas i nästa avsnitt för att definiera derivatan.

Vad händer med \( \,y \) när \( {\color{White} x} x \to - \infty {\color{White} |}\)?

Grafen visar ett ganska liknande beteende när \( x \, \) går mot "stora" negativa värden, dvs när \( x \to \, {\color{Red} {- \infty}} \): Även där går \( f(x)\, \) mot \( 0\, \) när \( x\, \) går mot \( {\color{Red} {- \infty}} \). I termer av limes:

\[ \lim_{x \to \, {\color{Red} {- \infty}}}\,{10 \over x - 2}\,=\,0 \]

Skillnaden är bara att nu \( f(x)\, \) närmar sig \( 0 \, \) från negativt håll (nedifrån).

Resultatet är identiskt både när \( x\, \) går mot \( \infty \) och när \( x\, \) går mot \( -\infty \), nämligen att \( f(x) \to 0 \, \). Vi kan sammanfatta:

Gränsvärdet för \( {\color{White} x} {10 \over x\,-\,2} {\color{White} x} \) då \( \,x \) går mot \( \infty {\color{White} x} \) existerar    och är \( {\color{Red} 0} \),    kort:

\[ \lim_{x \to \infty}\,{10 \over x\,-\,2}\,=\,0 \]

Existens av gränsvärden

Vi stannar hos exemplet ovan, men byter frågeställning: Vi tittar inte längre på \( x \to \pm\infty \) utan på \( {\color{Red} {x = 2}} \, \):

Funktionen \( y = f(x) = \) \( {10 \over x\,-\,2} \) har följande graf: \( \qquad \)  

Vad händer med funktionen i punkten \( {\color{White} x} x = 2 {\color{White} x} \) ?

Kurvan skjuter upp i höjden å ena sidan och ner i "djupet" å andra sidan av punkten \( x = 2\, \), därför att \( {10 \over x\,-\,2} \):s nämnare blir \( 0\, \) för \( x = 2\, \). Dvs \( f(x)\, \) är inte definierad för \( x = 2\, \). Följaktligen visar grafen i \( x = 2\, \) en diskontinuitet av typ oändlighetsställe. Annars är \( f(x)\, \) kontinuerlig i hela sin definitionsmängd som består av alla \( x \neq 2\, \).

Vi vill nu undersöka hur man kan beskriva \( \,f(x)\):s beteende för \( \, x = 2 \) med hjälp av limes?

Som grafen visar \(-\) och beräkningar med funktionsuttrycket bekräftar \(-\) går \( f(x)\, \) mot \( +\, \infty \) när man närmar sig \( \, x = 2 \) från höger och mot \( -\, \infty \) när man närmar sig \( \, x = 2 \) från vänster. Om vi uttrycker detta med pilar ser det ut så här:

\[ {10 \over x - 2} \to +\, \infty \quad {\rm när} \; x \to 2^+ \qquad {\color{White} x} {\rm och} {\color{White} x} \qquad {10 \over x - 2} \to -\, \infty \quad {\rm när} \; x \to 2^- \]

där \( x \to 2^+ \) betyder att närma sig \( \, x = 2 \) från höger (\( \, x > 2 \)) och \( x \to 2^- \) att närma sig \( \, x = 2 \) från vänster (\( \, x < 2 \)).

Eftersom det finns två olika resultat beroende på om \( \, x \) går mot \( \, 2 \) från höger eller från vänster säger man:

Gränsvärdet för \( {\color{White} x} {10 \over x\,-\,2} {\color{White} x} \) då \( \,x \) går mot \( \, 2 {\color{White} x} \) existerar inte,     kort:

Gränsvärde saknas.

Funktionen går mot två olika håll när \( \, x \to 2 \). Men att gränsvärdet inte kan ha två olika värden för ett och samma \( \,x \) är uppenbart. Limes måste ha ett entydigt värde, annars existerar den inte.

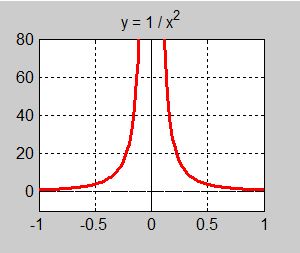
Men även om en funktion skulle gå mot t.ex. mot \( +\,\infty \), för ett visst \( \, x \) både från höger och vänster, t.ex. \( \displaystyle {f(x) = {1 \over x^2}} \) för \( \, x = 0 \), skulle det strikt matematiskt inte vara korrekt att säga att limes existerar och är \( +\,\infty \), därför att \( \infty \) inte är något värde. Med andra ord:

Ett gränsvärde måste, för att existera, vara både entydigt och ändligt.

Därför är det strikt matematiskt korrekt att säga: Gränsvärdena \( \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \) och \( \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \) saknas. Detta gäller i alla fall enligt en strikt definition av gränsvärdesbegreppet vars intuitiva innebörd återgavs ovan. Men det finns även andra typer av gränsvärden:

Ensidiga och oegentliga gränsvärden

Skiljer man däremot närmandet från höger till \( \, x = 2 \) från närmandet från vänster kan man bilda s.k. ensidiga gränsvärden:

\[ \lim_{x \to 2^{+}}\,{10 \over x - 2}\,=\,+\,\infty \qquad\quad {\color{White} x} {\rm och} {\color{White} x} \qquad\quad \lim_{x \to 2^{-}}\,{10 \over x - 2}\,=\,-\,\infty \]

där \( x \to 2^+ \) betyder att närma sig \( \, x = 2 \) från höger (\( \, x > 2 \)) och \( x \to 2^- \) att närma sig \( \, x = 2 \) från vänster (\( \, x < 2 \)).

Man pratar om höger- och vänstergränsvärdet genom att skilja mellan de två sätten att närma sig talet \( \, 2 \) på \( \, x\)-axeln: från höger \( x \to 2^+ \) och från vänster \( x \to 2^- \), därav beteckningen ensidig. I vårt exempel ger de också två olika resultat.

Gränsvärden av funktioner som går mot oändligheten (och därmed strikt talat inte existerar), men ändå skrivs med limessymbolen, kallar man oegentliga gränsvärden. Ett exempel på ett oegentligt gränsvärde är: \( \displaystyle {\lim_{x \to 0}\,{1 \over x^2}}\,=\,+\,\infty \) där funktionen \( \displaystyle f(x) = {1 \over x^2} \) (se grafen till höger) går mot \( +\,\infty \) både när \( \, x \to 0 \) från höger (\( \, x > 0 \)) och från vänster (\( \, x < 0 \)). Gränsvärdet är alltså entydigt men oändligt och därför oegentligt, till skillnad från \( \displaystyle f(x) = {10 \over x - 2} \) vars gränsvärde varken är entydigt eller ändligt när \( x \to 2 \) och därför inte existerar. Att man använder det ovannämnda skrivsättet för ensidiga och oegentliga gränsvärden sker av praktiska skäl. Man ersätter pilarna som vi använde inledningsvis med att beskriva gränsprocessen med limessymbolen istället. Det är bekvämt att använda en enhetlig notation för att beskriva gränsprocesser. Är man medveten om att limes enligt den strikta definitionen inte existerar är det o.k. OBS! Av skrivsättet för ensidiga och oegentliga gränsvärden följer fortfarande inte att \( \displaystyle {\lim_{x \to 2}\,{10 \over x - 2}} \) eller \( \displaystyle {\lim_{x \to 0}\,{1 \over x^2}} \) existerar.

Beräkning av gränsvärden

Exempel 1

Bestäm

\[ \lim_{x \to 0}\, {x^2 + 7\,x \over x} \]

Lösning:

För \( x = 0 \, \) är uttrycket under limes inte definierat. Därför måste vi faktorisera uttryckets täljare för att se om man ev. kan förkorta. Täljaren kan faktoriseras genom att bryta ut \( x \, \):

\[ \lim_{x \to 0}\, {x^2 + 7\,x \over x} \, = \, \lim_{x \to 0}\, {{\color{Red} x}\:(x + 7) \over {\color{Red} x}} \, = \, \lim_{x \to 0}\, (x + 7) \, = \, 0 + 7 \, = \, 7 \]

Exempel 2

a) Bestäm

\[ \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} \]

Lösning:

För att kunna bestämma limes måste vi först forma om uttrycket under limes:

\[ {4\,x\,+\,5 \over x} = {4\,{\color{Red} x} \over {\color{Red} x}} \,+\,{5 \over x} \,=\, 4 \,+\, {5 \over x} \]

Deluttrycket \( {5 \over x} \) går mot \( 0 \) både när \( x \to +\infty \) och \( x \to -\infty \):

\[ \lim_{x \to +\infty}\, {5 \over x} \, = \, \lim_{x \to -\infty}\, {5 \over x} \, = \, 0 \]

Därför kan vi nu bestämma limes för hela uttrycket:

\[ \lim_{x \to \infty}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to \infty}\, \left(4 \,+\, {5 \over x}\right) \,= \, 4\,+\,0 \,= \, 4\]

b) Bestäm

\[ \lim_{x \to 0}\, {4\,x\,+\,5 \over x} \]

Lösning:

\[ \lim_{x \to 0^+}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^+}\, \left(4 \,+\, {5 \over x}\right) \,= \, +\infty \]

\[ \lim_{x \to 0^-}\, {4\,x\,+\,5 \over x} \, = \, \lim_{x \to 0^-}\, \left(4 \,+\, {5 \over x}\right) \,= \, -\infty \]

där \( x \to 0^+ \) betyder att närma sig \( \, x = 0 \) från höger (\( \, x > 0 \)) och \( x \to 0^- \) att närma sig \( \, x = 0 \) från vänster (\( \, x < 0 \)).

Svar: Gränsvärde saknas.

Exempel 3

Bestäm

\[ \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} \]

Lösning:

För \( x = 2 \, \) är uttrycket under limes inte definierat. Därför måste vi faktorisera uttryckets täljare och nämnare för att se om man ev. kan förkorta. Täljaren kan faktoriseras med hjälp av konjugatreglen och nämnaren genom att bryta ut:

\[ x^2\,-\,4 = (x\,+\,2)\cdot(x\,-\,2) \]

\[ 5\,x - 10 = 5\,(x\,-\,2) \]

Nu kan vi förkorta uttrycket och bestämma limes:

\[ \lim_{x \to 2}\, {x^2\,-\,4 \over 5\,x - 10} \, = \, \lim_{x \to 2}\, {(x + 2) \cdot {\color{Red} {(x-2)}} \over 5\,{\color{Red} {(x-2)}}} \, = \, \lim_{x \to 2} \, {x + 2 \over 5} \, = \, {2 + 2 \over 5} \, = \, {4 \over 5} \, = \, 0,8 \]

Exempel 4

Bestäm

\[ \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \]

Lösning:

Här måste vi, för att förenkla uttrycket under limes, dividera uttryckets täljare och nämnare med den högsta \( \,x\)-potensen. Närmare bestämt betyder detta att dividera alla termer i uttryckets täljare och nämnare med \( \,x^3 \):

\[ \lim_{x \to \infty}\,\, {x^3\,-\,2 \over 2\,x^3\,+\,3\,x\,-\,4} \,=\, \lim_{x \to \infty}\,\, {x^3/x^3\,-\,2/x^3 \over 2\,x^3/x^3\,+\,3\,x/x^3\,-\,4/x^3} \,=\, \lim_{x \to \infty}\,\, {1\,-\,2/x^3 \over 2\,+\,3/x^2\,-\,4/x^3} \,=\, {1\,-\,0 \over 2\,+\,0\,-\,0} \,=\, {1 \over 2} \]

I sista skedet av förenklingen ovan har vi använt att:

\[ \lim_{x \to \infty}\, {2 \over x^3} \, = \, \lim_{x \to \infty}\, {3 \over x^2} \, = \, \lim_{x \to \infty} \, {4 \over x^3} \, = \, 0 \]

Exempel 5

Bestäm

\[ \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} \]

Lösning:

Vi måste faktorisera uttryckets täljare för att se om man ev. kan förkorta mot nämnaren:

\[ x^2 - x - 6 = 0 \, \]

För lösningarna \( x_1\,\) och \( x_2\,\) måste enligt Vieta gälla:

\[ \begin{align} x_1 + x_2 & = -(-1) = 1 \\ x_1 \cdot x_2 & = - 6 \end{align}\]

Vi måste alltså hitta två tal vars produkt är \( -6 \, \) och vars summa är \( 1 \, \). Med lite provande hittar man \( 3 \, \) och \( -2 \, \) eftersom \( 3 + (-2) = 1\, \) och \( 3 \cdot (-2) = -6 \):

\[ \begin{align} x_1 & = 3 \\ x_2 & = - 2 \end{align}\]

Täljarens faktorisering blir då:

\[ x^2 - x - 6 = (x - 3) \cdot (x + 2) \]

Nu kan vi förkorta uttrycket mot nämnaren och bestämma limes:

\[ \lim_{x \to 3}\, {x^2 - x - 6 \over x - 3} \, = \, \lim_{x \to 3}\, {{\color{Red} {(x-3)}} \cdot (x + 2) \over {\color{Red} {(x-3)}}} \, = \, \lim_{x \to 3}\, (x + 2) \, = \, 3 + 2 \, = \, 5 \]

Exempel 6

Följande funktion är given:

\[ y = f(x) = x^2 \]

Bestäm

\[ \displaystyle \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} \]

Lösning:

\[ f(2+h) = (2+h)^2 = 4 + 4\,h + h^2 \]

\[ \lim_{h \to 0}\,\,{f(2+h) - f(2) \over h} = \lim_{h \to 0} {(2+h)^2 - 2^2 \over h} = \lim_{h \to 0} {4 + 4\,h + h^2\,\,-\,\,4 \over h} = \lim_{h \to 0} {4\,h + h^2 \over h} = \]

\[ = \lim_{h \to 0} {{\color{Red} h}\,(4 + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (4 + h) = 4 \]

Exempel 7

Följande funktion är given:

\[ y = f(x) = x^2 \]

Bestäm

\[ \displaystyle \lim_{h \to 0}\,\,{f(x+h) - f(x) \over h} \]

Lösning:

Eftersom uttrycket under limes involverar två variabler \( x\, \) och \( h\, \) kommer limes, om den existerar, inte längre vara ett tal utan ett uttryck i \( x\, \), därför att gränsvärdet ska bildas för \( h \to 0 \). Under gränsprocessen kan \( x\, \) anses som en konstant.

\[ f(x+h) = (x+h)^2 = x^2 + 2\,x\,h + h^2 \]

\[ \lim_{h \to 0}\,\,{f(x+h) - f(x) \over h} = \lim_{h \to 0} {(x+h)^2 - x^2 \over h} = \lim_{h \to 0} {x^2 + 2\,x\,h + h^2 \, - \, x^2 \over h} = \lim_{h \to 0} {2\,x\,h + h^2 \over h} = \]

\[ = \lim_{h \to 0} {{\color{Red} h}\,(2\,x + h) \over {\color{Red} h}} = \lim_{h \to 0} \, (2\,x + h) = 2\,x \]

Observera att Exempel 6 är ett specialfall av Exempel 7 för \( x = 2 \, \).

Internetlänkar

https://www.youtube.com/watch?v=_oPD-c8IAzs

https://www.youtube.com/watch?v=StP64lMXZjA

https://www.youtube.com/watch?v=fPOX0QX8AH0

Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.