2.4 Derivatans definition

Innehåll

1 Exempel 1 Oljetank
2 Från genomsnittlig till momentan förändringshastighet
3 Från sekanten till tangenten
4 Derivatan som gränsvärde
5 Derivatan som funktion
6 Internetlänkar

Exempel 1 Oljetank

I avsnittet Genomsnittlig förändringshastighet betraktade vi följande problem:

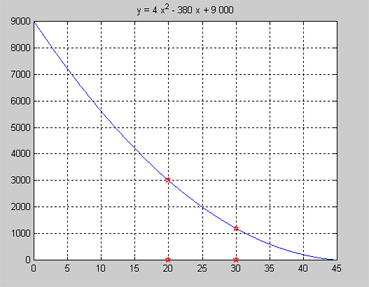
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen (grafen till höger):

\[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \]

där \( {\color{White} x} \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)

\[ y \, = \, {\rm Oljans\;volym\;i\;liter} \]

Beräkna oljans exakta dvs momentana utströmningshastighet när den är störst.

Lösning:

Grafen visar att kurvans lutning är störst i \( x = 0\, \) dvs den största utströmningshastigheten antas vid tiden \( x = 0\, \) när oljan har mest volym. Vi ska alltså beräkna:

Oljans momentana utströmningshastighet i \( x = 0\, \).

Med andra ord: Vi ska nu gå över från genomsnittlig till momentan förändringshastighet.

Från genomsnittlig till momentan förändringshastighet

Enligt den allmänna definitionen till genomsnittlig förändringshastighet

Från sekanten till tangenten

Fil:DerivatDef1 50.jpg

Derivatan som gränsvärde

Fil:DerivatDef2 50.jpg

Derivatan som funktion

Fil:DerivatDef3 50.jpg

En annan notation för derivatan av en funktion \( y = f(x)\, \) som anknyter till \( \displaystyle {\Delta y \over \Delta x} \), är \( \displaystyle {dy \over dx} \) vilket vi dock inte kommer att använda så ofta.