Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 26: | Rad 26: | ||
:::<math> y \, = \, {\rm Oljans\;volym\;i\;liter} </math> | :::<math> y \, = \, {\rm Oljans\;volym\;i\;liter} </math> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen: | ||
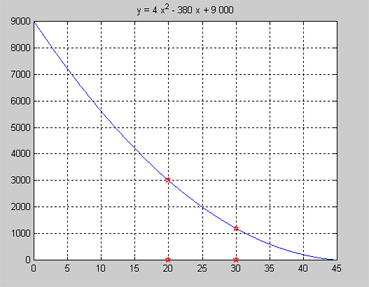
| + | :::<math> y \, = \, 4\,x^2 - 380\,x + 9\,000 </math> | ||
| + | där <math> {\color{White} x} \quad \! x \, = \, {\rm Tiden\;i\;minuter} </math> | ||
| + | |||
| + | :::<math> y \, = \, {\rm Oljans\;volym\;i\;liter} </math> | ||
| + | |||
| + | '''a)''' Rita grafen till funktionen som beskriver utströmningen. | ||
| + | |||
| + | '''b)''' Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet från början tills tanken är tom. | ||
| + | |||
| + | '''c)''' Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet <math> 20 \leq x \leq 30 </math>. | ||
| + | |||
| + | '''d)''' När är oljans (genomsnittliga) utströmningshastighet störst? Ange den så noggrant som möjligt. | ||
| + | |||
| + | '''Lösning''': | ||
| + | |||
| + | '''a)''' Se grafen till höger. | ||
| + | </td> | ||
| + | <td>[[Image: Ex2_70.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
== Från sekanten till tangenten == | == Från sekanten till tangenten == | ||
Versionen från 1 oktober 2014 kl. 11.36
| <-- Förra avsnitt | Teori | Övningar | Nästa avsnitt --> |
Lektion 13 Derivatans definition
Innehåll
Exempel 1 Oljetank
I avsnittet Genomsnittlig förändringshastighet betraktade vi följande problem:
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
- \[ y \, = \, 4\,x^2 - 380\,x + 9\,000 \]
där \( {\color{White} x} \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)
- \[ y \, = \, {\rm Oljans\;volym\;i\;liter} \]
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
där \( {\color{White} x} \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)
a) Rita grafen till funktionen som beskriver utströmningen. b) Hur stor är oljans genomsnittliga utströmningshastighet i hela tidsintervallet från början tills tanken är tom. c) Beräkna oljans genomsnittliga utströmningshastighet i tidsintervallet \( 20 \leq x \leq 30 \). d) När är oljans (genomsnittliga) utströmningshastighet störst? Ange den så noggrant som möjligt. Lösning: a) Se grafen till höger. |
 |
Från sekanten till tangenten
Derivatan som gränsvärde
Derivatan som funktion
En annan notation för derivatan av en funktion \( y = f(x)\, \) som anknyter till \( \displaystyle {\Delta y \over \Delta x} \), är \( \displaystyle {dy \over dx} \) vilket vi dock inte kommer att använda så ofta.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.
