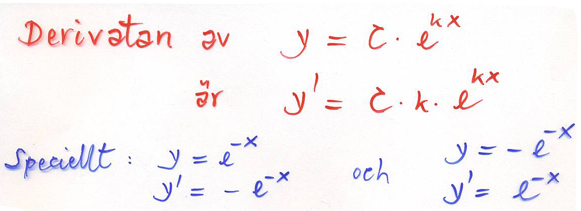Skillnad mellan versioner av "2.6 Derivatan av exponentialfunktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 9: | Rad 9: | ||
| − | [[File: | + | [[File: Lektion 21 Deriv Expfkt Ruta.pdf|<strong><span style="color:blue">Lektion 21 Derivatan av exponentialfunktioner</span></strong>]] |
__TOC__ | __TOC__ | ||
Versionen från 10 november 2014 kl. 15.20
| <-- Förra avsnitt | Teori | Övningar | Nästa avsnitt --> |
Lektion 21 Derivatan av exponentialfunktioner
Innehåll
Derivatan av exponentialfunktionen \( y = e\,^x \)
Det kan vara bra att friska upp sina kunskaper om exponentialfunktionen med basen \( e\, \) (Eulers tal) från kapitel 1. Vi behöver nämligen i detta avsnitt att härleda derivatan av exponentialfunktionen \( y = e\,^x \) med basen \( e\, \) för att sedan kunna med hjälp av den ställa upp deriveringsregeln för den allmänna exponentialfunktionen \( y = a\,^x \) med en godtycklig bas \( a > 0\, \).
För att kunna göra det gör vi först ett försök att hjälp av med derivatans definition ställa upp en deriveringsregel för \( y = a\,^x \). Vi kan redan säga nu: Försöket kommer att misslyckas, vilket dock kommer att leda oss till den avgörande frågeställning som kommer att lösa problemet. Denna frågeställning vänder på steken: Istället för att fråga efter deriveringsregeln, ger man en deriveringsregel \(-\) den enklaste möjliga, nämligen derivatan = funktionen \(-\) och frågar efter en bas som gör att denna deriveringsregel gäller. Frågeställningen lyder:
Svaret är: Ja, om och endast om \( {\color{White} x} a \, = \, e \) . Detta är möjligt eftersom vi har friheten att välja en bas.
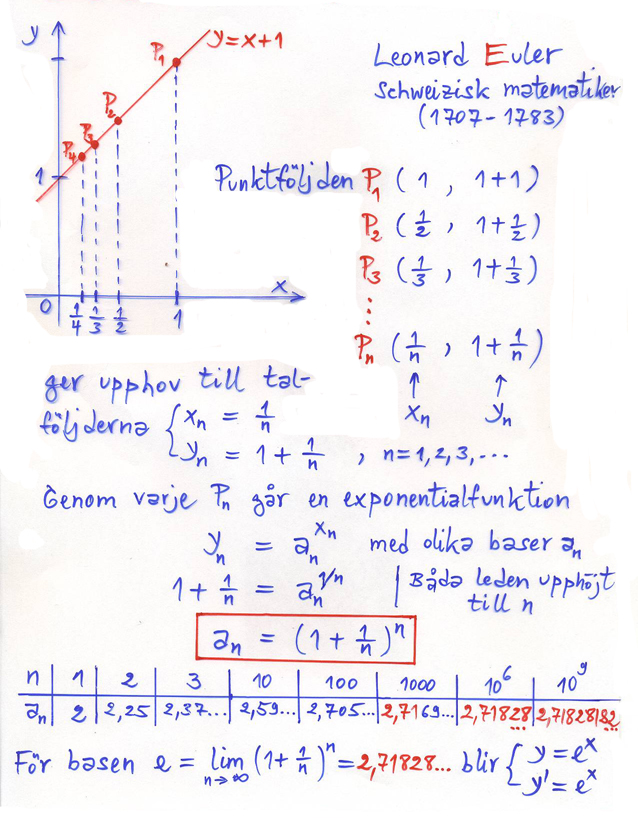
Frågeställningen har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet \( e\, \) som vi använde i Hur kom(mer) talet \( e \,\) till? På 1700-talet bevisade Euler att den efterfrågade basen var just \( e\, \), varför talet kallats efter honom. Eulers formel kan vi nu \(-\) efter att ha behandlat limesbegreppet \(-\) formulera så här:
- \[ \lim_{x \to \infty} {\left(1 + {1 \over x}\right)^x} \; =\; e \; = \; 2,718281828\cdots \]
Vi försöker i detta avsnitt att följa Eulers bevis för denna formel.
Misslyckat försök med derivatans definition
Tangenten till \( y = e\,^x \) i punkten \( \,x = 0 \)
Vi antar att det finns en bas \( \,e \) \(-\) som än så länge är okänd \(-\) så att:
- \[\begin{array}{lclcl} y & = & f\,(x) & = & e\,^x \\ y\,' & = & f\,'\,(x) & = & e\,^x \end{array}\]
Ekvationen för tangenten till kurvan \( y = e\,^x \) i punkten \( \,x = 0 \) har \(\,k\)-formen \( y \, = \, k\,x \, + \, m \) .
För att bestämma \( \, k \) konstaterar vi att tangenten till kurvan \( y = e\,^x \) i \( \,x = 0 \) har samma lutning \(\,k\) som själva kurvan i denna punkt, nämligen \( f\,'(0) \). Därför:
- \[ k \, = \, f\,'(0) \, = \, e\,^0\, = \, 1 \]
Således blir tangentens ekvation \( y \, = \, x \, + \, m \) .
För att bestämma \( \, m \) sätter vi in beröringspunktens koordinater
- \[ x = 0 \]
- \[ y = f(0) = e\,^0 = 1 \]
i tangentens ekvation och beräknar \( \, m \):
- \[\begin{array}{rcl} y & = & x \, + \, m \\ 1 & = & 0 \, + \, m \\ 1 & = & m \end{array}\]
Då blir tangentens ekvation:
- \[ y \, = \, x \, + \, 1 \]
Eulers bevis
På denna tangent konstruerar vi en punktföljd \( P_1, \, P_2, \, P_3, \, \ldots \) vars \( \,x\)-koordinater bildar talföljden
- \[ 1, \, {1 \over 2}, \, {1 \over 3}, \, {1 \over 4}, \, \ldots \qquad {\rm med\;den\;allmänna \;termen} \qquad x_n \, = \, {1 \over n} \qquad \mbox{där} \;\; n = 1,\,2,\,3,\,\cdots \]
Se även tabellen i Hur kom(mer) talet \( e \,\) till?
Vi har fått följande resultat:
Derivatan av exponentialfunktionen med basen \( \, e \)
- \[ \begin{array}{llcl} {\rm Om} & y & = & e\,^x \;\; {\rm där} \;\; e = {\rm Eulers\;tal} \\ {\rm då} & y\,' & = & e\,^x \end{array}\]
Deriveringsregeln för \( y = C\,e\,^{k\,x} \)
Derivatan av den allmänna exponentialfunktionen \( y = a\,^x \)
Från att ha ställt upp deriveringsregeln för exponentialfunktionen \( y = e\,^x \) är det bara ett enkelt steg till deriveringsregeln för den allmänna exponentialfunktionen \( y = a\,^x \) med en godtycklig bas \( a > 0\, \):
Specialfallet \( a = e\, \) och \( \ln a = \ln e = 1\, \) ger derveringsregeln \( y\,' = e^x \) för exponentialfunktionen med basen \( e\, \).
Uppdaterad tabell över deriveringsregler
Vi utvidgar tabellen över deriveringsregler från förra avsnitt med våra nya resultat i detta avsnitt. I följande tabell är \( C,\,c,\,a,\,k,\,m,\,n \) konstanter medan \( x\, \) och \( y\, \) är variabler:
\( y\, \) \( y\,' \) \( c\, \) \( 0\, \) \( x\, \) \( 1\, \) \( a\; x \) \( a\, \) \( k\; x \, + \, m \) \( k\, \) \( x^2\, \) \( 2\,x \) \( a\,x^2 \) \( 2\,a\,x \) \( x^n\, \) \( n\cdot x\,^{n-1} \) \( a\,x\,^n \) \( a\cdot n\cdot x\,^{n-1} \) \( \displaystyle {1 \over x} \) \( \displaystyle - {1 \over x^2} \) \( \sqrt{x} \) \( \displaystyle {1 \over 2\, \sqrt{x}} \) \( e\,^x \) \( e\,^x \) \( e\,^{k\,x} \) \( k\cdot e\,^{k\,x} \) \( C\cdot e\,^{k\,x} \) \( C\cdot k\cdot e\,^{k\,x} \) \( a\,^x \) \( a\,^x \cdot \ln a \) \( C\cdot a\,^{k\,x} \) \( C\cdot k\cdot a\,^{k\,x} \cdot \ln a \) \( f(x) + g(x)\, \) \( f\,'(x) + g\,'(x) \) \( a\cdot f(x) \) \( a\cdot f\,'(x) \)
De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner \( f(x)\, \) och \( g(x)\, \). Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna. Denna tabell kommer att ytterligare kompletteras i Matte 4-kursen då vi kommer att lära oss fler deriveringsregler, speciellt regler för derivatan av en produkt resp. kvot av funktioner, den s.k. produkt- resp. kvotregeln.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.