Skillnad mellan versioner av "2.4 Derivatans definition"
Taifun (Diskussion | bidrag) m (→Exempel 1 Oljetank) |
Taifun (Diskussion | bidrag) m (→Exempel 1 Oljetank) |
||
| Rad 37: | Rad 37: | ||
::::::<big> Oljans <strong><span style="color:red">momentana</span></strong> utströmningshastighet i <math> x = 0\, </math>.</big> | ::::::<big> Oljans <strong><span style="color:red">momentana</span></strong> utströmningshastighet i <math> x = 0\, </math>.</big> | ||
| − | Det ska vi nu göra genom att gå över från genomsnittlig | + | Det ska vi nu göra genom att gå över från genomsnittlig [[2.2_Genomsnittlig_förändringshastighet#Exempel_2_Oljetank|<strong><span style="color:blue">(Exempel 2 d)</span></strong>]] till <strong><span style="color:red">momentan</span></strong> förändringshastighet. |
</td> | </td> | ||
<td>[[Image: Ex2_70.jpg]]</td> | <td>[[Image: Ex2_70.jpg]]</td> | ||
Versionen från 2 oktober 2014 kl. 09.33
| <-- Förra avsnitt | Teori | Övningar | Nästa avsnitt --> |
Lektion 13 Derivatans definition
Innehåll
Exempel 1 Oljetank
| I avsnittet Genomsnittlig förändringshastighet betraktade vi följande problem:
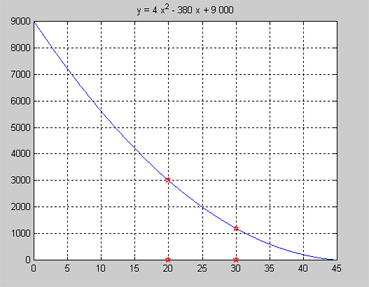
En oljetank läcker genom ett hål i tankens botten. Utströmningen av oljan beskrivs av funktionen:
där \( {\color{White} x} \quad \! x \, = \, {\rm Tiden\;i\;minuter} \)
Beräkna oljans exakta dvs momentana utströmningshastighet när den är störst. Lösning: Grafen visar att kurvans lutning är störst i \( x = 0\, \), vilket innebär att den största utströmningshastigheten antas vid tiden \( x = 0\, \) när oljan har mest volym (\( 9\,000 \)) lite och trycket på hålet är störst. Vi ska alltså beräkna:
Det ska vi nu göra genom att gå över från genomsnittlig (Exempel 2 d) till momentan förändringshastighet. |
 |
Från genomsnittlig till momentan förändringshastighet
Den allmänna definitionen till genomsnittlig förändringshastighet är:
- \[ {\Delta y \over \Delta x} \; = \; {f(x_1 + h) \, - \, f(x_1) \over h} \qquad {\rm i\;\;intervallet } \qquad x_1 \,\leq\, x \,\leq\, x_1 + h \]
Vi beräknar först oljans genomsnittliga utströmningshastighet i intervallet \( 0 \,\leq\, x \,\leq\, h \):
- \[ {\Delta y \over \Delta x} = {f(h) \, - \, f(0) \over h} = {4\,h^2 - 380\,h + 9\,000 \,-\, 9\,000 \over h} \]
Från sekanten till tangenten
Derivatan som gränsvärde
Derivatan som funktion
En annan notation för derivatan av en funktion \( y = f(x)\, \) som anknyter till \( \displaystyle {\Delta y \over \Delta x} \), är \( \displaystyle {dy \over dx} \) vilket vi dock inte kommer att använda så ofta.
Internetlänkar
http://www.youtube.com/watch?v=OyKmc2bPWe0
http://www.youtube.com/watch?v=8of_svLfcjk
http://www.youtube.com/watch?v=OY8CeLUxE64&feature=related
http://www.youtube.com/watch?v=2wH-g60EJ18&feature=related
http://www.larcentrum.org/Safir/MA1203W/htm/m03_deriv1/m03_deriv_definition.htm
http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=129&Itemid=132
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.