Skillnad mellan versioner av "1.2 Faktorisering av polynom"

Från Mathonline
Hoppa till: navigering, sök
m (→‎Polynom i faktorform)
m
 
(186 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[Repetition Faktorisering & Vieta från Matte 2|Repetition Faktorisering & Vieta]]}}
+
{{Not selected tab|[[1.2 Repetition Faktorisering & Vieta från Matte 2|Repetition: Faktorisering & Vieta]]}}
 
{{Selected tab|[[1.2 Faktorisering av polynom|Teori]]}}
 
{{Selected tab|[[1.2 Faktorisering av polynom|Teori]]}}
 
{{Not selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}}
 
{{Not selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}}
 
{{Not selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}}
 
{{Not selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}}
−
{{Not selected tab|[[1.1 Internetlänkar till Faktorisering av Polynom|Internetlänkar]]}}
+
{{Not selected tab|[[1.3 Rationella uttryck|Nästa avsnitt -->]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
| style="border-bottom:1px solid #797979"  width="100%"|  
 
|}
 
|}
 +
[[1.1 Polynom|<span style="color:blue"><-- Förra avsnitt</span>]]
  
  
 +
[[Media: Lektion_3_Faktorisering_av_polynom_Rutaa.pdf|<strong><span style="color:blue">Lektion 3 Faktorisering av polynom</span></strong>]]
  
−
[[Media: Lektion 5 Faktorisering av polynom.pdf|Lektion 3 Faktorisering av polynom I]]
+
[[Media: Lektion_4_Faktorisering_av_polynomFa_Ruta.pdf|<strong><span style="color:blue">Lektion 4 Faktorisering av polynom: Fördjupning</span></strong>]]
 +
 
 +
__TOC__
  
−
[[Media: Lektion 6 Faktorisering av polynom2.pdf|Lektion 4 Faktorisering av polynom II]]
 
  
 
== Polynom i faktorform ==
 
== Polynom i faktorform ==
  
−
Låt oss titta på följande exempel på faktorisering av ett polynom: 
+
=== Exempel ===
  
−
::::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
+
Vi betraktar följande likhet ([[Repetition_Faktorisering_%26_Vieta_från_Matte_2#Exempel_1|<strong><span style="color:blue">Exempel 1</span></strong>]] från tidigare): 
  
−
Till vänster om likhetstecknet har vi ett polynom som en summa av termer. Till höger står samma polynom som en produkt av faktorer dvs i faktorform. Detta <strong><span style="color:red">polynom i faktorform</span></strong> är resultat av faktorisering. Ingredienserna i faktorformen dvs faktorerna <math> (x-3)\, </math> och <math> (x-4)\, </math> är i sin tur polynom, fast av mindre grad, nämligen 1. Ursprungspolynomet är av grad 2, liknande faktorerna 3 och 4 som är mindre än 12. Man har splittrat upp det hela i sina beståndsdelar: talet 12 i sina beståndsdelar 3 och 4 och polynomet <math> x^2 - 7\,x + 12 </math> i sina beståndsdelar <math> (x-3)\, </math> och <math> (x-4)\, </math>.
+
::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
  
−
Matematiskt inser man likheten ovan genom att utveckla högerledet:  
+
Man inser likheten ovan genom att utveckla högerledet:  
  
−
:::::::<math> (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 </math>
+
:::<math> (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 </math>
  
−
Men hur får man fram faktorformen från polynomet? Dvs hur faktoriserar man ett polynom? Frågan är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets [[1.1_Polynom#Ett_polynoms_nollst.C3.A4llen|<strong><span style="color:blue">nollställen</span></strong>]]. För att förstå varför faktorisering avslöjar polynomets nollställen sätter vi polynomet <math> x^2 - 7\,x + 12 </math> till 0 och får följande ekvation:
+
Till höger har vi ett polynom som en summa av termer. Till vänster står samma polynom som en produkt av faktorer dvs ett <strong><span style="color:red">polynom i faktorform</span></strong>.  
  
−
::::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 </math>
+
Faktorformen (produkten) är resultat av faktorisering av polynomet (summan). Polynomet är av grad 2, medan ingredienserna i faktorformen dvs <math> (x-3)\, </math> och <math> (x-4)\, </math> är polynom av grad 1. Man kan jämföra det med faktoriseringen <math> 12 = 3 \cdot 4\, </math>. Faktorerna 3 och 4 är mindre än 12. Man har splittrat upp det hela i sina beståndsdelar: talet 12 i sina beståndsdelar 3 och 4 och polynomet <math> x^2 - 7\,x + 12 </math> i sina beståndsdelar <math> (x-3)\, </math> och <math> (x-4)\, </math>.
  
−
Denna ekvation är en inbjudan att söka de tal <math> x\,</math> för vilka polynomets värde är <math> 0\,</math>. Därför är denna ekvations lösningar identiska med polynomets nollställen, vare sig man skriver polynomet som en summa av termer eller i faktorform. Faktorformen <math>(x-3) \cdot (x-4) </math> har dock den stora fördelen att man kan se lösningarna till ekvationen ovan utan att behöva räkna:
+
Men hur får man fram faktorformen från polynomet? Dvs hur faktoriserar man ett polynom? Frågan är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets [[1.1_Polynom#Ett_polynoms_nollst.C3.A4llen|<strong><span style="color:blue">nollställen</span></strong>]]. För att förstå varför faktorisering avslöjar polynomets nollställen sätter vi polynomet <math> x^2 - 7\,x + 12 </math> till 0 och får följande ekvation:
  
−
<strong><span style="color:red">Nollproduktmetoden</span></strong> visar att <math> 3\,</math> och <math> 4\,</math> är lösningar till ekvationen <math> (x-3) \cdot (x-4) = 0 </math>. Så här resonerar nollproduktmetoden: För att produkten <math> (x-3) \cdot (x-4) </math> ska vara lika med <math> 0\,</math> måste antingen den första faktorn <math> (x-3)\, </math> eller den andra faktorn <math> (x-4)\, </math> vara lika med <math> 0\,</math>. För att <math> (x-3)\, </math> eller <math> (x-4)\, </math> ska vara lika med <math> 0\,</math> måste <math> x\, </math> antingen vara lika med <math> 3\,</math> eller lika med <math> 4\,</math>. Detta i sin tur innebär att <math> 3\,</math> och <math> 4\,</math> är lösningar till ekvationen <math> (x-3) \cdot (x-4) = 0 </math>. Å andra sidan: Pga likheten mellan polynom och dess faktorform måste <math> 3\,</math> och <math> 4\,</math> även vara polynomets nollställen och därmed lösningar till ekvationen:
+
::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 </math>
  
−
::::::::::<math> x^2 - 7\,x + 12 = 0 </math>
+
Denna ekvation är en inbjudan att söka de tal <math> x\,</math> för vilka polynomets värde är <math> 0\,</math>. Därför är denna ekvations lösningar identiska med polynomets nollställen, vare sig man skriver polynomet som en summa av termer eller i faktorform. Faktorformen <math>(x-3) \cdot (x-4) </math> har dock den stora fördelen att man kan se lösningarna till ekvationen ovan utan att behöva räkna: Det är nollproduktmetoden som vi lärde oss i Matte 2 som visar att <math> 3\,</math> och <math> 4\,</math> är lösningar till ekvationen <math> (x-3) \cdot (x-4) = 0 </math>. Här en påminnelse:
  
−
I det här exemplet hade vi redan faktorformen och diskuterade i efterhand likheten med polynomet och dess konsekvenser. Men vad gör man om man inte än har faktorformen? Hur får man fram den?
+
==== Nollproduktmetoden ====
  
−
== Faktorisering av 2:a gradspolynom ==
+
Så här resonerar nollproduktmetoden:
  
−
Resonemanget ovan ger oss nu en metod i handen for att få fram faktorformen från polynomet. För att faktorisera polynomet<math> x^2 - 7\,x + 12 </math> behöver vi bara beräkna dess nollställen, säg <math> x_1\, </math> och <math> x_2\, </math>, och sedan skriva upp faktorformen <math>(x-x_1)\cdot (x-x_2) </math>. Låt oss genomföra det i vårt exempel:  
+
* Vi har ekvationen:
  
−
::::::::::<math>\begin{align} x^2 - 7\,x + 12 & = 0                          \\
+
::::::<math> (x-3) \cdot (x-4) \, = \, 0 </math>
−
                                      x_{1,2} & = 3,5 \pm \sqrt{12,25 - 12}  \\
+
−
                                      x_{1,2} & = 3,5 \pm \sqrt{0,25}        \\
+
−
                                      x_{1,2} & = 3,5 \pm 0,5                \\
+
−
                                      x_1    & = 4                          \\
+
−
                                      x_2    & = 3                          \\
+
−
          \end{align}</math>
+
  
−
Därför har polynomet <math> x^2 - 7\,x + 12 </math> faktorformen <math> (x-3) \cdot (x-4) </math>. Vi kommer att lära oss en effektivare metod för lösning av 2:a gradsekvationer och därmed för faktorisering av 2:gradspolynom, när vi lärt oss ett enkelt samband mellan ett polynoms koefficienter och dess nollställen (Vietas formler).
+
* För att produkten i vänsterledet ska vara lika med <math> 0\,</math> måste antingen den första faktorn <math> (x-3)\, </math> eller den andra faktorn <math> (x-4)\, </math> vara lika med <math> 0\,</math>.  
  
−
Det som vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:
+
* För att <math> (x-3)\, </math> eller <math> (x-4)\, </math> ska vara lika med <math> 0\,</math> måste <math> x\, </math> antingen vara lika med <math> 3\,</math> eller lika med <math> 4\,</math>.
  
−
'''Sats (Faktorisering med 2 nollställen)''':
+
* Detta i sin tur innebär att <math> 3\,</math> och <math> 4\,</math> är lösningar till ekvationen ovan.
−
::::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> har nollställena <math> x_1\, </math> och <math> x_2\, </math> så gäller:</big>
+
  
−
:::::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math>
+
Pga likheten mellan polynom och dess faktorform (se ovan) måste <math> 3\,</math> och <math> 4\,</math> även vara polynomets nollställen och därmed lösningar till ekvationen:
  
−
För att bevisa satsen ovan kan man t.ex. sätta in 2:a gradsekvationens lösningsformel (pq-formeln) för <math> x_1\, </math> och <math> x_2\, </math> och utveckla produkten på högerledet. En jämförelse av koefficienter kommer att resultera i likhet med vänsterledet. Det finns motsvarande satser om polynom av högre grad än 2 som vi inte behandlar här.
+
::::::<math> x^2 - 7\,x + 12 = 0 </math>
  
−
Istället ska vi undersöka ett enkelt, men intressant samband mellan 2:a gradspolynomets koefficienter <math> p\, </math> och <math> q\, </math> och dess nollställen <math> x_1\, </math> och <math> x_2\, </math>, vilket ger dig möjligheten att roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp den 2:a gradsekvation vars lösningar just är 3 och 4.
+
I det här exemplet hade vi redan faktorformen och diskuterade i efterhand likheten med polynomet och dess konsekvenser. Men vad gör man om man inte än har faktorformen? Hur får man fram den?
  
−
== Dubbelrot ==
 
  
−
'''Sats (Faktorisering med 1 nollställe)''':
+
== Faktorisering av 2:a gradspolynom ==
−
::::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> endast har ett nollställe <math> x_1\, </math> så gäller:</big>
+
  
−
::::::::<math> x^2 + p\,x + q = (x-x_1)^2 </math>
+
Resonemanget ovan ger oss följande metod i handen for att få fram faktorformen från polynomet.
  
−
::::<big>Ett sådant nollställe kallas för <span style="color:red">dubbelrot</span> till ekvationen <math> x^2 + p\,x + q = 0 </math>.</big>
+
<b>Exempel:</b> Faktorisera polynomet <math> x^2 - 7\,x + 12 </math>
  
−
Dubbelrötter har vissa intressanta egenskaper. Låt oss börja att upptäcka dem genom att rita grafen till polynomfunktionen och undersöka på vilket sätt dubbelroten "skär" x-axeln. Vi tar polynomet från Exempel 2 ovan där ekvationen <math> x^2 - 6\,x + 9 = 0 </math> hade dubbelroten x = 3.
+
<b>Lösning:</b> Hitta polynomets nollställen dvs ställ upp och lös 2:a gradsekvationen:
  
−
Så här ser grafen ut till polynomfunktionen <math> y = x^2 - 6\,x + 9 </math>:
+
::::::<math> x^2 - 7\,x + 12 = 0 </math>
  
−
[[Image: Dubbelrot_70.jpg]]
+
För lösningarna <math> x_1\,</math> och <math> x_2\,</math> gäller enligt [[Repetition_Faktorisering_%26_Vieta_från_Matte_2#Vietas_formler_-_samband_mellan_koefficienter_och_nollst.C3.A4llen|<strong><span style="color:blue">Vietas formler</span></strong>]]:
  
−
Grafen visar att kurvan inte skär utan bara berör x-axeln vid x = 3. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära x-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:
+
::::::<math> \begin{align} x_1  +  x_2 & = -(-7) = 7  \\
 +
                          x_1 \cdot x_2 & = 12
 +
            \end{align}</math>
  
−
:::::::::::<math> x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 </math>
+
Dvs vi behöver hitta två tal vars produkt är 12 och vars summa är 7. Med lite provande hittar man:
  
−
Den dubbla förekomsten av faktorn (x-3) ger roten dess namn dubbelrot. Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.
+
::::::<math>\begin{align}  x_1 & = 3 \\
 +
                          x_2 & = 4
 +
              \end{align}</math>
  
−
== Det allmänna fallet (icke-normalform) ==
+
eftersom <math> 3 + 4 = 7\, </math> och <math> 3 \cdot 4 = 12 </math>. Därmed är polynomets faktorisering:
  
−
Alla våra hittills behandlade polynom var i normalform, dvs den ledande koefficienten (kvadratiska termens koefficient eller talet framför x²) var alltid 1. Det behöver inte alltid vara så. Låt oss t.ex. faktorisera följande polynom med ledande koefficienten 3:
+
::::::<math> x^2 - 7\,x + 12 = \underline{(x - 3) \cdot (x - 4)} </math>
  
−
:::::::::::::::::<math> 3\,x^2 - 6\,x - 9 </math>
 
  
−
Lösningen består i att återföra problemet till den kända typen i normalform genom att bryta ut den ledande koefficienten:
+
Självklart hade man kunnat använda även p-q-formeln för att lösa 2:a gradsekvationen. Då hade det sett ut så här:
  
−
::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) </math>
+
::::::<math>\begin{array}{rcl} x^2 - 7\,x + 12 & = & 0                          \\
 +
                                      x_{1,2} & = & 3,5 \pm \sqrt{12,25 - 12}  \\
 +
                                      x_{1,2} & = & 3,5 \pm \sqrt{0,25}        \\
 +
                                      x_{1,2} & = & 3,5 \pm 0,5                \\
 +
                                      x_1    & = & 3                          \\
 +
                                      x_2    & = & 4                         
 +
            \end{array}</math>
  
−
Vi faktoriserar först det nya polynomet <math> x^2 - 2\,x - 3 </math> som är i normalform enligt:
+
Man ser just i det här fallet att Vieta är enklare och snabbare. Enklare aritmetik har den stora praktiska fördelen att risken för felräkning minimeras.
  
−
::::::::::<math> x^2 - 2\,x - 3 = (x-x_1) \cdot (x-x_2) </math>
+
Det vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:
  
−
Efter att ha löst detta nya problem kan vi gå tillbaka till det ursprungliga problemet för att få faktoriseringen av <math> 3\,x^2 - 6\,x - 9 </math>.
 
  
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> som ger oss faktoriseringen av <math> x^2 - 2\,x - 3 </math> kan vi som vanligt använda Vietas formler:
+
----
 +
'''Sats (Faktorisering med 2 nollställen)''':
 +
::<big>Om 2:gradspolynomet <math> x^2 + p\,x + q </math> har nollställena <math> x_1\, </math> och <math> x_2\, </math> så gäller:
  
−
<math> \begin{align} x_1  +   x_2 & = -(-2) = 2  \\
+
:::::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math>
−
                      x_1 \cdot x_2 & = -3
+
</big>
−
        \end{align}</math>
+
För att bevisa satsen ovan kan man t.ex. sätta in p-q-formeln för <math> x_1\, </math> och <math> x_2\, </math>, utveckla produkten på högerledet och genomföra jämförelse av koefficienter, se [[1.2_Övningar_till_Faktorisering_av_polynom#.C3.96vning_13|<strong><span style="color:blue">övn. 13</span></strong>]].
  
−
Man hittar lösningarna <math> x_1 = 3\,</math> och <math> x_2 = -1\,</math> eftersom <math> 3 + (-1) = 2\,</math> och <math> 3 \cdot (-1) = -3 </math>.
+
Det finns motsvarande satser om polynom av högre grad än 2, se  [[1.2_Fördjupning_till_Faktorisering_av_Polynom#Algebrans_fundamentalsats|<strong><span style="color:blue">Algebrans fundamentalsats</span></strong>]].
 +
----
  
−
Därför kan polynomet <math> x^2 - 2\,x - 3 </math> faktoriseras så här:
 
  
−
<math> x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) </math>
+
== Rotens olika betydelser ==
  
−
Går vi tillbaka och sätter in denna lösning i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
Ordet <b>rot</b> har i matematiken olika betydelser i olika sammanhang:
  
−
::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math>
+
* Räkneoperationen rotdragning med rottecknet <math> {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} </math> som symbol, t.ex. roten ur <math> 4\, </math> är <math> 2\, </math> osv.
  
−
Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering.
+
* Lösningen av en ekvation. I ekvationssammanhang är rot synonym till en ekvations lösning. T.ex. är <math> x_1 = 2\, </math> och <math> x_2 = -2\, </math> rötter dvs lösningar till ekvationen <math> x^2 = 4\, </math>.
  
−
===== Exempel 3 =====
+
* Nollstället till ett polynom. I polynomsammanhang är rot synonym till ett polynoms nollställe. I exemplet ovan är <math> x_1 = 2\, </math> och <math> x_2 = -2\, </math> rötter dvs nollställen till polynomet <math> x^2 - 4\, </math>.
  
−
Vad gör man om den ledande koefficienten "inte går att bryta ut" eftersom den inte delar de andra koefficienterna jämnt? Man gör det ändå och går över till tal i bråkform. Det finns nämligen ingen begränsning varken för polynomets nollställen eller koefficienter, när det gäller taltypen: De kan vara heltal, som var fallet hittills i våra exempel, men även bråk- eller decimaltal. Låt oss t.ex. faktorisera följande polynom med en ledande koefficient som inte delar de andra koefficienterna jämnt:
+
Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten.
  
−
:::::::::::::::::<math> 7\,x^2 - 5\,x - 2 </math>
 
  
−
Vi bryter ut 7 och skriver det nya polynomets koefficienter i bråkform:
+
== Dubbelrot ==
−
 
+
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x-x_1) \cdot (x-x_2) </math>
+
−
 
+
−
För att få fram <math> x_1\,</math> och <math> x_2\,</math> använder vi Vietas formler:
+
−
 
+
−
<math> \begin{align} x_1  +  x_2 & = {5 \over 7}  \\
+
−
                    x_1 \cdot x_2 & = - {2 \over 7}
+
−
        \end{align}</math>
+
−
 
+
−
Man hittar lösningarna <math> x_1 = 1\,</math> och <math> x_2 = -{2 \over 7}\,</math> eftersom <math> 1 - {2 \over 7} = {5 \over 7} </math> och <math> 1 \cdot {-2 \over 7} = {-2 \over 7} </math>.
+
−
 
+
−
Så får vi det nya polynomets faktorisering:
+
−
 
+
−
<math> x^2 - {5 \over 7}\,x - {2 \over 7} = (x - 1) \cdot (x + {2 \over 7}) </math>
+
−
 
+
−
Går vi tillbaka och sätter in detta i det ursprungliga problemets ansats får vi det ursprungliga polynomets faktorisering:
+
−
 
+
−
::::::::::<math> 7\,x^2 - 5\,x - 2 = 7\,(x^2 - {5 \over 7}\,x - {2 \over 7}) = 7\,(x - 1) \cdot (x + {2 \over 7}) </math>
+
−
 
+
−
Vill man i slutet bli av med bråktal kan man multiplicera in 7 i den andra parentesen och skriva faktoriseringen så här:
+
−
 
+
−
:::::::::::::<math> 7\,x^2 - 5\,x - 2 = (x - 1) \cdot (7\,x + 2) </math>
+
−
 
+
−
== Faktorisering av 3:e och högre gradspolynom ==
+
−
 
+
−
Faktorisering av 2:a gradspolynom är alltid möjlig för oss eftersom vi kan lösa 2:a gradsekvationer. I de fall man lyckas återföra 3:e eller högre gradsekvationer till 2:a gradsekvationer är det även möjligt att faktorisera polynom av högre grad än 2. Ett sådant fall föreligger om man antingen känner till eller t.ex. med hjälp av grafen kan få fram åtminstone en lösning till en 3:e gradsekvation. Låt oss genomföra detta för följande exempel:
+
−
 
+
−
'''Problem:''' Faktorisera 3:e gradspolynomet
+
−
 
+
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 </math>
+
−
 
+
−
'''Lösning:''' För att få fram något av polynomets nollställen ritar vi
+
−
 
+
−
grafen till funktionen <math> y = x^3 - 6\,x^2 + 5\,x + 12 </math>
+
−
 
+
−
[[Image: 3e_gradspolynom_70.jpg]]
+
−
 
+
−
Grafen visar att polynomet har tre nollställen av vilka ett är ganska tydligt på bilden och kan avläsas till x = -1, medan de andra två är mindre tydliga. För att avgöra om detta nollställe är exakt gör vi en prövning genom att sätta in x = -1 i polynomet:
+
−
 
+
−
<math> P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -1 -6 -5 +12 = -12 +12 = 0 </math>
+
−
 
+
−
Prövningen visar att x = -1 är ett exakt nollställe till P(x). Härav kan vi nu dra slutsatsen att de två andra nollställena måste uppfylla följande ekvation:
+
−
 
+
−
:::::::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = 0 </math>
+
−
 
+
−
där <math> Q(x) </math> är ett 2:a gradspolynom som vi inte känner till än. Denna slutsats baseras på en generell matematisk sats, algebrans fundamentalsats som säger att ett polynom av grad n har n nollställen. Vi kan med nollproduktmetoden resonera så här: För att produkten <math> Q(x) \cdot (x+1) </math> ska vara lika med 0 måste antingen <math> Q(x) </math> eller <math> (x+1) </math> vara lika med 0. Vi vet redan att <math> (x+1) </math> är 0 för x = -1  som är <math> P(x) </math>:s ena nollställe. Alltså måste <math> P(x) </math>:s andra två nollställen finnas i <math> Q(x) </math>. Med andra ord de andra två nollställen måste vara det 2:a gradspolynomet <math> Q(x) </math>:s nollställen. Kan vi bestämma <math> Q(x) </math>, beräkna dess nollställen samt ställa upp dess faktorform, har vi faktoriserat även det 3:e gradspolynomet <math> P(x) </math>. Vi har ju redan hittat ett nollställe och ställt upp en ansats till faktoriseringen av <math> P(x) </math> i form av ekvationen ovan. Vi bearbetar nu vidare denna ansats genom att införa i den för <math> Q(x) </math> den allmänna formen för ett 2:a gradspolynom:
+
−
 
+
−
<math> Q(x) = a\,x^2 + b\,x + c </math>
+
−
 
+
−
där a, b och c är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:
+
−
 
+
−
::::::<math> x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) </math>
+
−
 
+
−
Vi vet från förra avsnitt att två polynom är lika med varandra om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer. För att kunna genomföra denna jämförelse av koefficienter utvecklar vi produkten på höger sidan och ordnar termerna:
+
−
 
+
−
::<math> x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c </math>
+
−
 
+
−
Jämförelse av koefficienterna på höger- och vänsterled ger:
+
−
 
+
−
::<math> \begin{align} a    & = 1    \\
+
−
                      b + a & = -6  \\
+
−
                      c + b & = 5    \\
+
−
                      c    & = 12
+
−
        \end{align}</math>
+
  
−
Genom insättning av <math> a = 1 </math> i den andra och <math> c = 12 </math> i den tredje ekvationen får vi i båda fall b = -7. Därmed har vi bestämt polynomet <math>Q(x)</math>:
+
När vi nu i fortsättningen pratar om en dubbelrot menar vi två lösningar till en ekvation som sammanfaller, vilket även kan uppfattas som endast en lösning.
  
−
<math> Q(x) = x^2 - 7\,x + 12 </math>
 
  
−
I början av detta avsnitt (Faktorisering av 2:a gradspolynom) hade vi faktoriserat det här polynomet till:
+
----
 +
'''Sats (Faktorisering med 1 nollställe)''':<big>
 +
::Om 2:gradspolynomet <math> x^2 + p\,x + q </math> endast har ett nollställe <math> x_1\, </math> så gäller:
  
−
::::::::<math> x^2 - 7\,x + 12 = (x-3) \cdot (x-4) </math>
+
:::::::::<math> x^2 + p\,x + q = (x-x_1)^2 </math>
  
−
Inför vi nu detta resultat i vår ansats i början får vi faktoriseringen för P(x):
+
::Ett sådant nollställe kallas för <strong><span style="color:red">dubbelrot</span></strong> till ekvationen <math> x^2 + p\,x + q = 0 </math>.
 +
----
 +
</big>
  
−
::<math> P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = (x-3)\,\cdot\,(x-4)\,\cdot\,(x+1) </math>
 
  
−
Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3. Anledningen till det är algebrans fundamentalsats som vi redan nämnde tidigare och som lite förenklad lyder så här:
+
==== Exempel ====
  
−
== Algebrans fundamentalsats ==
+
Polynomet <math> x^2 - 6\,x + 9 </math> har dubbelroten <math> x = 3\, </math> eftersom ekvationen <math> x^2 - 6\,x + 9 = 0 </math> har endast lösningen <math> x = 3\, </math>, se [[Repetition_Faktorisering_%26_Vieta_från_Matte_2#Exempel_3|<strong><span style="color:blue">Exempel 3</span></strong>]] från repetitionen om Vieta.
  
−
'''Sats''':
+
Dubbelrötter har vissa intressanta egenskaper. En av dem kan vi se när vi ritar grafen till polynomfunktionen och undersöker på vilket sätt dubbelroten "skär" <math> \, x</math>-axeln.
−
::::<big>Ett polynom av grad n har exakt n nollställen <math> x_1, \, x_2, \,\quad\ldots\, x_n </math>och kan faktoriseras så här:</big>
+
  
−
:::<math> a_n \, x^n \,+\, a_{n-1} \, x^{n-1} + \quad \ldots \quad + a_1 \, x \,+\, a_0\;=\;a_n \cdot\, (x-x_1) \,\cdot\, (x-x_2) \,\cdot\quad\ldots\quad \cdot\, (x-x_n) </math>  
+
<big>Grafen till polynomfunktionen</big> <math> {\color{White} x} y = x^2 - 6\,x + 9 \; {\rm :} \quad\quad </math> [[Image: Dubbelrot_70.jpg]]
  
−
Anmärkningar:
 
−
* Egentligen utgör endast den första delen (polynom av grad n har exakt n nollställen) algebrans fundamentalsats. Den andra delen om faktorisering är en följd av den.
 
−
* Antalet n nollställen är räknade med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
 
−
* Den fullständiga faktoriseringen i linjära faktorer <math> (x-x_i)\, </math> är endast möjlig i mängden av s.k. komplexa tal, en taltyp som inte behandlas i C-kursen. För oss som räknar med reella tal (största taltyp vi känner till) betyder der att vissa polynom endast kan faktoriseras till linjära och kvadratiska faktorer.
 
  
−
===== Exempel 4 =====
+
Grafen visar att kurvan inte skär utan bara <strong><span style="color:black">berör</span></strong> <math>\,x</math>-axeln vid <math> x = 3\, </math>. Dvs det finns endast <strong><span style="color:black">en</span></strong> gemensam punkt mellan kurvan och <math>\,x</math>-axeln. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära <math>\,x</math>-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:
  
−
<math> P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) </math>
+
::::::<math> x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 </math>
  
−
Polynomet P(x) har en dubbelrot x = 0, en enkel rot x = 1 och två s.k. komplexa rötter som ger upphov till den kvadratiska faktor som står sist. För oss räcker det att ange faktoriseringen i forman ovan. Vi kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten x = 0 får vi genom att bryta ut <math> x^2 </math>, roten x = 1 kan vi t.ex. få via grafen samt en prövning. Den kvadratiska faktorns koefficienter kan vi beräkna med hjälp av jämförelse av koefficienter. Att det inte går att få fram en fullständig faktorisering i linjära faktorer beror på att den kvadratiska faktorn saknar reella rötter.
+
Det intressanta med dubelrötter är att vi endast har <b>en</b> lösning <math> x = 3\, </math> till 2:a gradsekvationen <math> x^2 - 6 x + 9 = 0\, </math>. Fast, om vi tittar på faktorformen <math> (x - 3) \cdot (x - 3) = 0 </math> kan man lika bra säga att vi har två identiska lösningar eller två som sammanfaller - ett filosofiskt dilemma som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot.
  
−
===== Exempel 5 =====
+
Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.
  
−
Att vi ändå kan ha praktisk nytta av algebrans fundamentalsats visar följande exempel: I [[1.1 Övning 6|övning 6]] i avsnittet 1.1 Ekvationer hade vi (förhoppningsvis) löst 4:e gradsekvationen
 
  
−
<math> x^4 - 29\;x^2 = -100 </math>
+
== Internetlänkar ==
  
−
och fått lösningarna
+
http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx
  
−
<math> x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 </math>
+
http://mathworld.wolfram.com/PolynomialFactorization.html
  
−
Vi kan skriva ekvationen som en polynomekvation
+
http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html
  
−
<math> P(x) = x^4 - 29\;x^2 + 100 = 0 </math>
+
http://www.sosmath.com/algebra/factor/fac04/fac04.html
  
−
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet P(x) så här:
+
http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf
  
−
<math> P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) </math>
 
  
  
  
 
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved.
 
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved.

Nuvarande version från 15 oktober 2014 kl. 11.09

       Repetition: Faktorisering & Vieta          Teori          Övningar          Fördjupning          Nästa avsnitt -->      

<-- Förra avsnitt


Lektion 3 Faktorisering av polynom

Lektion 4 Faktorisering av polynom: Fördjupning


Polynom i faktorform

Exempel

Vi betraktar följande likhet (Exempel 1 från tidigare):

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]

Man inser likheten ovan genom att utveckla högerledet:

\[ (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 \]

Till höger har vi ett polynom som en summa av termer. Till vänster står samma polynom som en produkt av faktorer dvs ett polynom i faktorform.

Faktorformen (produkten) är resultat av faktorisering av polynomet (summan). Polynomet är av grad 2, medan ingredienserna i faktorformen dvs \( (x-3)\, \) och \( (x-4)\, \) är polynom av grad 1. Man kan jämföra det med faktoriseringen \( 12 = 3 \cdot 4\, \). Faktorerna 3 och 4 är mindre än 12. Man har splittrat upp det hela i sina beståndsdelar: talet 12 i sina beståndsdelar 3 och 4 och polynomet \( x^2 - 7\,x + 12 \) i sina beståndsdelar \( (x-3)\, \) och \( (x-4)\, \).

Men hur får man fram faktorformen från polynomet? Dvs hur faktoriserar man ett polynom? Frågan är relevant av olika skäl: För det första tillåter faktorformen förkortning och därmed förenkling av komplexa algebraiska uttryck. För det andra avslöjar faktorformen polynomets nollställen. För att förstå varför faktorisering avslöjar polynomets nollställen sätter vi polynomet \( x^2 - 7\,x + 12 \) till 0 och får följande ekvation:

\[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 \]

Denna ekvation är en inbjudan att söka de tal \( x\,\) för vilka polynomets värde är \( 0\,\). Därför är denna ekvations lösningar identiska med polynomets nollställen, vare sig man skriver polynomet som en summa av termer eller i faktorform. Faktorformen \((x-3) \cdot (x-4) \) har dock den stora fördelen att man kan se lösningarna till ekvationen ovan utan att behöva räkna: Det är nollproduktmetoden som vi lärde oss i Matte 2 som visar att \( 3\,\) och \( 4\,\) är lösningar till ekvationen \( (x-3) \cdot (x-4) = 0 \). Här en påminnelse:

Nollproduktmetoden

Så här resonerar nollproduktmetoden:

  • Vi har ekvationen:
\[ (x-3) \cdot (x-4) \, = \, 0 \]
  • För att produkten i vänsterledet ska vara lika med \( 0\,\) måste antingen den första faktorn \( (x-3)\, \) eller den andra faktorn \( (x-4)\, \) vara lika med \( 0\,\).
  • För att \( (x-3)\, \) eller \( (x-4)\, \) ska vara lika med \( 0\,\) måste \( x\, \) antingen vara lika med \( 3\,\) eller lika med \( 4\,\).
  • Detta i sin tur innebär att \( 3\,\) och \( 4\,\) är lösningar till ekvationen ovan.

Pga likheten mellan polynom och dess faktorform (se ovan) måste \( 3\,\) och \( 4\,\) även vara polynomets nollställen och därmed lösningar till ekvationen:

\[ x^2 - 7\,x + 12 = 0 \]

I det här exemplet hade vi redan faktorformen och diskuterade i efterhand likheten med polynomet och dess konsekvenser. Men vad gör man om man inte än har faktorformen? Hur får man fram den?


Faktorisering av 2:a gradspolynom

Resonemanget ovan ger oss följande metod i handen for att få fram faktorformen från polynomet.

Exempel: Faktorisera polynomet \( x^2 - 7\,x + 12 \)

Lösning: Hitta polynomets nollställen dvs ställ upp och lös 2:a gradsekvationen:

\[ x^2 - 7\,x + 12 = 0 \]

För lösningarna \( x_1\,\) och \( x_2\,\) gäller enligt Vietas formler:

\[ \begin{align} x_1 + x_2 & = -(-7) = 7 \\ x_1 \cdot x_2 & = 12 \end{align}\]

Dvs vi behöver hitta två tal vars produkt är 12 och vars summa är 7. Med lite provande hittar man:

\[\begin{align} x_1 & = 3 \\ x_2 & = 4 \end{align}\]

eftersom \( 3 + 4 = 7\, \) och \( 3 \cdot 4 = 12 \). Därmed är polynomets faktorisering:

\[ x^2 - 7\,x + 12 = \underline{(x - 3) \cdot (x - 4)} \]


Självklart hade man kunnat använda även p-q-formeln för att lösa 2:a gradsekvationen. Då hade det sett ut så här:

\[\begin{array}{rcl} x^2 - 7\,x + 12 & = & 0 \\ x_{1,2} & = & 3,5 \pm \sqrt{12,25 - 12} \\ x_{1,2} & = & 3,5 \pm \sqrt{0,25} \\ x_{1,2} & = & 3,5 \pm 0,5 \\ x_1 & = & 3 \\ x_2 & = & 4 \end{array}\]

Man ser just i det här fallet att Vieta är enklare och snabbare. Enklare aritmetik har den stora praktiska fördelen att risken för felräkning minimeras.

Det vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom, åtminstone sådana som är givna i normalform:


Sats (Faktorisering med 2 nollställen):

Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:
\[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]

För att bevisa satsen ovan kan man t.ex. sätta in p-q-formeln för \( x_1\, \) och \( x_2\, \), utveckla produkten på högerledet och genomföra jämförelse av koefficienter, se övn. 13.

Det finns motsvarande satser om polynom av högre grad än 2, se Algebrans fundamentalsats.


Rotens olika betydelser

Ordet rot har i matematiken olika betydelser i olika sammanhang:

  • Räkneoperationen rotdragning med rottecknet \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) som symbol, t.ex. roten ur \( 4\, \) är \( 2\, \) osv.
  • Lösningen av en ekvation. I ekvationssammanhang är rot synonym till en ekvations lösning. T.ex. är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs lösningar till ekvationen \( x^2 = 4\, \).
  • Nollstället till ett polynom. I polynomsammanhang är rot synonym till ett polynoms nollställe. I exemplet ovan är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs nollställen till polynomet \( x^2 - 4\, \).

Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten.


Dubbelrot

När vi nu i fortsättningen pratar om en dubbelrot menar vi två lösningar till en ekvation som sammanfaller, vilket även kan uppfattas som endast en lösning.


Sats (Faktorisering med 1 nollställe):

Om 2:gradspolynomet \( x^2 + p\,x + q \) endast har ett nollställe \( x_1\, \) så gäller:
\[ x^2 + p\,x + q = (x-x_1)^2 \]
Ett sådant nollställe kallas för dubbelrot till ekvationen \( x^2 + p\,x + q = 0 \).


Exempel

Polynomet \( x^2 - 6\,x + 9 \) har dubbelroten \( x = 3\, \) eftersom ekvationen \( x^2 - 6\,x + 9 = 0 \) har endast lösningen \( x = 3\, \), se Exempel 3 från repetitionen om Vieta.

Dubbelrötter har vissa intressanta egenskaper. En av dem kan vi se när vi ritar grafen till polynomfunktionen och undersöker på vilket sätt dubbelroten "skär" \( \, x\)-axeln.

Grafen till polynomfunktionen \( {\color{White} x} y = x^2 - 6\,x + 9 \; {\rm :} \quad\quad \) 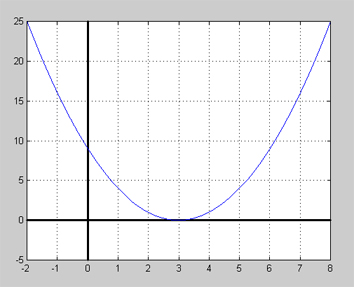Dubbelrot 70.jpg


Grafen visar att kurvan inte skär utan bara berör \(\,x\)-axeln vid \( x = 3\, \). Dvs det finns endast en gemensam punkt mellan kurvan och \(\,x\)-axeln. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära \(\,x\)-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:

\[ x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 \]

Det intressanta med dubelrötter är att vi endast har en lösning \( x = 3\, \) till 2:a gradsekvationen \( x^2 - 6 x + 9 = 0\, \). Fast, om vi tittar på faktorformen \( (x - 3) \cdot (x - 3) = 0 \) kan man lika bra säga att vi har två identiska lösningar eller två som sammanfaller - ett filosofiskt dilemma som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot.

Andra viktiga egenskaper av dubbelrötter kommer vi att lära känna senare när vi i kapitel 2 behandlar derivering.


Internetlänkar

http://tutorial.math.lamar.edu/Classes/Alg/Factoring.aspx

http://mathworld.wolfram.com/PolynomialFactorization.html

http://www.mathsisfun.com/algebra/fundamental-theorem-algebra.html

http://www.sosmath.com/algebra/factor/fac04/fac04.html

http://www.lboro.ac.uk/research/helm/C_HELM_backup_24nov03/helm_website/documents/wb03_blk3.pdf



Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.

Hämtad från "https://matte5.mathonline.se/index.php?title=1.2_Faktorisering_av_polynom&oldid=16132"