1.3 Fördjupning till Rationella uttryck

Repetition: Bråkräkning

Teori

Övningar

Fördjupning

Nästa avsnitt -->

<-- Förra avsnitt

Lektion 5 Rationella uttryck

Lektion 6 Rationella uttryck: Fördjupning

Rationella tal och rationella uttryck

Ordet ratio betyder i matematiken förhållandet eller kvoten (resultatet av division) mellan två heltal. Men:

Division av heltal resulterar i regel utanför mängden av heltal. T.ex. är \( 3 \over 4 \) inte längre ett heltal. För att kunna räkna vidare måste vi utvidga mängden av heltal.

Det blir redan nödvändigt att utvidga talbegreppet från heltal till bråktal för att t.ex. kunna lösa följande ekvation som involverar endast heltal:

\[\begin{align} 4 \cdot x & = 3 \\ \\ x & = {3 \over 4} \end{align} \]

Men ekvationens lösning är inte längre heltal utan ett rationellt tal. Vi har kommit till en ny talmängd, mängden av rationella tal, dvs alla tal som kan skrivas i bråkform.

På liknande sätt utvidgar man funktionsbegreppet från polynom till rationella uttryck för att t.ex. kunna lösa följande "ekvation" (på ett högre plan) som involverar endast polynom och vars "obekant" är \(R(x)\,\):

\[\begin{align} (x^2 - 1)\cdot R(x) & = 6\,x \\ \\ R(x) & = {6\,x \over x^2 - 1} \end{align} \]

De kända delarna i "ekvationen" ovan är polynomen \(x^2-1\,\) och \(6\,x\), men "lösningen" \(R(x)\,\) är inte längre polynom utan ett rationellt uttryck. Vi har kommit till en ny mängd av uttryck, mängden av rationella uttryck, dvs alla uttryck som kan skrivas som en kvot mellan två polynom. Att \(R(x)\,\) är ett rationellt uttryck beror på att det består av kvoten mellan de två polynomen \(6\,x\) och \(x^2-1\,\).

Division av två polynom ger i regel inget polynom utan ett rationellt uttryck, se Övningar till Polynom, övn 1 d). Precis som division av två heltal i regel inte ger ett heltal utan ett rationellt tal.

Övergången från polynom till rationella uttryck är i många avseenden jämförbar med övergången från heltal till rationella tal. Analogin mellan heltal och polynom å ena sidan och rationella tal och rationella uttryck å andra sidan är inte begränsad till det här exemplet utan går mycket längre. Den är både intressant ur teoretiskt perspektiv och nyttig ur praktisk synvinkel.

Varför är division med 0 inte definierad?

Både i rationella tal och rationella uttryck får nämnaren inte bli \( 0\, \) eftersom division med \( 0\, \) inte är definierad.

Division med 0 är den viktigaste "förbjudna" operationen i matematiken. Men vad beror det på att det är "förbjudet"? När vi besvarar denna fråga kommer vi också att inse att det snarare är en omöjlighet än ett förbud.

Praktisk förklaring

Ta fram din miniräknare och mata in:

\[ 1 \over 0 \]

Du kommer att få ERROR. Räknaren kan inte genomföra denna operation. Varför?

Fortsätt dina experiment med räknaren genom att dela \( 1\, \) inte direkt med \( 0\, \) utan med små tal. Och låt dessa små tal bli mindre och mindre:

\( x\, \)	\( {1 \over x} \)
\( 0,1\, \)	\( 10\, \)
\( 0,01\, \)	\( 100\, \)
\( 0,001\, \)	\( 1000\, \)
\( 0,000\,1 \)	\( 10\,000 \)
\( 0,000\,01 \)	\( 100\,000 \)
\( 0,000\,001 \)	\( 1\,000\,000 \)
\( 0,000\,000\,1 \)	\( 10\,000\,000 \)
\( 0,000\,000\,01 \)	\( 100\,000\,000 \)
\( \cdots \)	\( \cdots \)
\( \rightarrow 0 \)	\( \rightarrow \infty \)

Experimentet visar: Ju mindre \( x\, \) blir desto större blir \( {1 \over x} \). I gränsfallet \( x = 0\, \) blir \( {1 \over x} \) oändligt stort.

\( \infty \) är symbolen för oändligheten. Men det är fel att skriva:

\[ {\rm {\color{Red} {OBS!\;Fel:}}} \quad\; {1 \over 0} = \infty \]

Detta är ingen korrekt matematisk notation. Ett tal kan inte vara lika med \( \infty \) därför att \( \infty \) inte är något tal utan endast en symbol. Korrekt ser det ut så här:

\[ {\rm {\color{Red} {Rätt:}}} \qquad\quad\, {1 \over x} \to \infty \quad {\rm när} \quad x \to 0 \]

Och läses så här \( {1 \over x} \) går mot \( \infty \) när \( x\, \) går mot \( 0\, \).

Slutsats: \( {\color{White} x} {1 \over 0} \) är inget tal och därför inte definierat.

Teoretisk förklaring

Vad betyder \( 12 / 4 \) ?

\[ 12 / 4 = {\color{Red} x} \quad {\rm betyder: \quad Att\;hitta\;ett\;tal\;}{\color{Red} x}\; {\rm så\;att\;} {\color{Red} x} \cdot 4 = 12 \]

Uppenbarligen är detta tal \( {\color{White} x} {\color{Red} {x = 3} {\color{White} x} } \) därför att \( {\color{Red} 3} \cdot 4 = 12 \).

Vad betyder \( 12 / 0 \) ?

\[ 12 / 0 = {\color{Red} x} \quad {\rm betyder: \quad Att\;hitta\;ett\;tal\;}{\color{Red} x}\; {\rm så\;att\;} {\color{Red} x} \cdot 0 = 12 \]

Men det finns inget sådant tal \( {\color{Red} x} \) därför att \( {\color{White} x} {\color{Red} x} \cdot 0 = 0 {\color{White} x} \neq 12 \).

Slutsats:     Operationen \( 12 / 0 \,\) och därmed division med \( 0 \,\) är omöjligt att genomföra.

Rationella funktioner

Ett bra sätt att studera rationella uttryck är att bilda funktioner med dem genom att tilldela dem en annan variabel, t.ex. \( y\, \). Fördelen med funktioner är är att man kan visualisera dem med grafer.

Exempel 1

Det enklast tänkbara exemplet på ett rationellt uttryck är:

\[ 1 \over x \]

Uttrycket är rationellt därför att det är en kvot mellan polynomet \( 1\, \) (av graden 0) och polynomet \( x\, \) (av graden 1). När vi tilldelar det variabeln \( y\, \) ger uttrycket upphov till den rationella funktionen:

\[ y = {1 \over x} \]

En rationell funktion är alltså kvoten mellan två polynom som tilldelas en variabel \( y\, \).

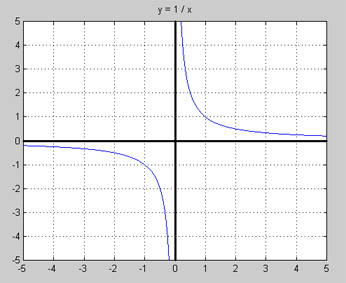
\( y = \) \( {1 \over x} \) har en graf vars förlopp markant skiljer sig från polynomfunktioners utseende:

Den väsentliga skillnaden mellan denna graf och polynomfunktioners graf är att den här har två skilda grenar, medan en polynomfunktions graf har ett sammanhängande förlopp. Uttryckt i matematiska termer säger man att en polynomfunktion är kontinuerlig. Ett polynoms graf kan ritas utan att man lyfter pennan från papperet, medan i grafen ovan måste vid \( x = 0\, \) pennan lyftas för att gå från grafens ena gren till den andra. Dvs grafen är inte sammanhängande i \( x = 0\, \). Man säger att funktionen är icke-kontinuerlig i \( x = 0\, \).

Den matematiska anledningen till denna diskontinuitet är att funktionen \( y = \) \( {1 \over x} \) inte har något värde för \( x = 0\, \). Division med 0 ger inget tal och är därmed odefinierad. När \( x \, \) närmar sig \( 0\, \) går \( y\, \) mot oändligheten, vilket tydligt framgår av grafen. Man säger: Funktionen \( y = \) \( {1 \over x} \) är inte definierad för \( {\color{Red} x = 0}\, \). Man måste undanta \( x = 0\, \) från funktionens definitionsmängd, dvs \( y = \) \( {1 \over x} \) är definierad för alla \( x\, \) utom för \( x = 0\, \).

Icke-definierbarheten och diskontinuiteten för vissa \( x\, \) är något typiskt för alla rationella funktioner och det är det som skiljer dem från polynomfunktioner som är definierade och kontinuerliga för alla \( x\, \).

Exempel 2

Genom att understryka orden för vissa \( x\, \) ovan vill vi säga att det är bara några isolerade \(\,x\)-värden för vilka en rationell funktion kan vara odefinierad. Antalet sådana \(\,x\)-värden kan hos rationella funktioner vara 0, 1, 2, \(\ldots\). Antalet 0 innebär att det även finns rationella funktioner som inte har några \( x\, \) för vilka de är odefinierade, dvs de är definierade och kontinuerliga för alla \( x\, \) precis som vanliga polynom. Ett exempel på sådana "snälla" rationella funktioner är:

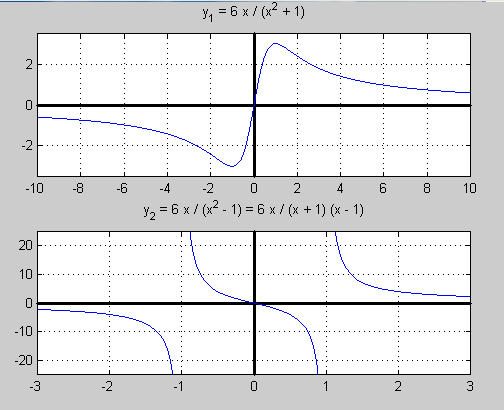
\[ y_1 = {6\,x \over x^2 + 1} \]

Anledningen till att \(y_1\,\) är definierad för alla \( x\, \) är att funktionsuttryckets nämnare, dvs polynomet \( x^2 + 1\, \) inte har några reella nollställen. Det i sin tur beror på att ekvationen
\( x^2 + 1 = 0\, \) saknar reell lösning därför att den ger \( x^2 = -1\, \) och roten ur \( -1\, \) inte är ett reellt tal. Grafen till funktionen \(y_1\,\) visar att \(y_1\,\) är definierad och kontinuerlig för alla \( x\, \) (övre kurvan) :

I den undre delen av bilden ovan har vi, för att kunna jämföra, även ritat grafen till en annan rationell funktion \(y_2\,\) som skiljer sig från \(y_1\,\) endast i ett förtecken i nämnaren:

\[ y_2 = {6\,x \over x^2 - 1} \]

Av samma skäl som nämndes för uttryck är denna funktion definierad för alla \( x\, \) utom för \( x = 1\, \) och \( x = -1\, \).

Skillnaden endast i ett förtecken i nämnaren räcker för att resultera i ett helt annorlunda beteende av funktionen \(y_2\,\) jämfört med \(y_1\,\). Som grafen visar är \(y_2\,\):s kurva uppdelad i tre grenar och har två ställen där den inte är sammanhängande (inte kontinuerlig). En blick på funktionsuttrycket avslöjar detta. Här kan vi dra nytta av faktorisering som vi lärt oss i förra avsnitt. Skriver man nämnarens polynom i faktorform ser man att att \(y_2\,\) varken är definierad för \( x_1 = -1\, \) eller för \( x_2 = 1\, \):

\[ y_2 = {6\,x \over x^2 - 1} = {6\,x \over (x + 1) \cdot (x - 1)} \]

När \( x\, \) närmar sig \( -1\, \) eller \( 1\, \) går \(y_2\,\) mot oändligheten, vilket även framgår av grafen. Exemplet visar att det som är väsentligt för rationella funktioner och därmed för rationella uttryck, är om polynomet i nämnaren har några nollställen och, om det är fallet, vilka de är. Med andra ord, om polynomet i nämnaren låter sig faktorisera eller ej. Om ja, kan vi genom faktorisering få fram nollställena. I vårt exempel kan man i \( y_1\, \) inte faktorisera \( x^2 + 1\, \) inom ramen av reella tal, för ekvationen \( x^2 + 1 = 0\, \) saknar reella lösningar. Däremot går det i \( y_2\, \) att faktorisera så här \( (x^2 - 1) = (x + 1) \cdot (x - 1) \), för ekvationen \( x^2 - 1 = 0\, \) har lösningarna \( x_1 = -1\, \) och \( x_2 = 1\, \).

Hävbara och icke-hävbara diskontinuiteter

Vi har hittills använt bråktalens räkneregler för att räkna med rationella uttryck utan att stöta på några hinder. Men vi får inte glömma att rationella uttryck ändå är komplexare objekt. Därför är det inte förvånansvärt att de har egenskaper som inte längre kan jämföras med motsvarigheter hos bråktal. En av dessa visas upp när man förkortar dem efter faktorisering av täljaren och nämnaren.

Efter faktorisering av täljaren och nämnaren samt förkortning med faktorn \( (x+3)\, \) förenklas det rationella uttrycket väsentligt. Men denna förkortning är endast korrekt om \( x \not= -3 \) eftersom förkortning med \( (x+3)\,\) innebär division med \( 0\,\) om \( x = -3\, \). Likhetstecknet mellan de rationella uttrycken gäller endast under förutsättningen \( x \not= -3 \). Det enklare uttrycket är identiskt med det ursprungliga inte för alla \( x\, \) utan för alla utom för \( x = -3\, \). Det blir ännu tydligare när vi betraktar dem som rationella funktioner. Då uppsår nämligen frågan: Vad händer med diskontinuiteten i \( x = -3\, \) som försvinner efter att vi förkortat uttrycket med faktorn \( (x+3)\, \)? Och vad är det för skillnad mellan diskontinuiteterna i \( x = -3\, \) och \( x = 3\, \)?

För att undersöka dessa frågor skriver vi dem som funktioner och ritar båda funktioners grafer:

\[\begin{align} y_3 = f(x) & = {2\,x^2 + 6\,x \over x^2 - 9} = {2\,x\,{\color{Red} {(x + 3)}} \over {\color{Red} {(x + 3)}}\,(x - 3)} \\ \\ y_4 = g(x) & = {2\,x \over x - 3}\end{align} \]

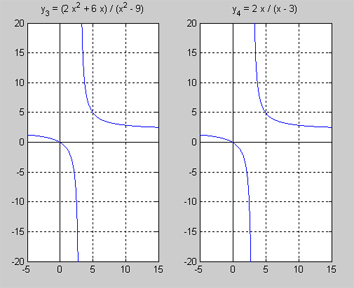
I den vänstra delen av bilden ser man grafen till funktionen \( f(x)\,\) och i den högra delen grafen till funktionen \( g(x)\,\). Till synes visar resultatet helt identiska kurvor. Men i själva verket vet vi att funktionen \( f(x)\, \) inte är definierad för \( x = -3\, \) och har en diskontinuitet där. Därför har dess graf (kurvan till vänster) ett "hål" eller en "lucka" i \( x = -3\, \) som man inte ser med blotta ögat. Så grafen lurar oss. Vi måste hålla oss till \( f(x)\, \):s funktionsuttryck ovan som klart visar två diskontinuiteter, en i \( x = -3\, \) och den andra i \( x = 3\, \). Den första som vi lyckades få bort genom förkortning, är en s.k. hävbar diskontinuitet medan den andra är icke-hävbar.

Kontinuerlig fortsättning

Hävbara diskontinuiteter är "snälla" och kan repareras. En ny funktion kan definieras som inte längre har den ursprungliga funktionens hävbara diskontinuiteter, men är annars identisk med den. En sådan funktion kallas den kontinuerliga fortsättningen av den ursprungliga.

I det här fallet skulle man kunna t.ex. komplettera funktionen \( f(x)\, \):s definition med ett värde för \( x = -3\, \) som gör att den nya funktionen blir kontinuerlig mot sin omgivning. Hur får man fram detta värde? Man gör det genom att först förkorta \( \,f(x)\):s funktionsuttryck med \( (x+3\,) \) och få \( g(x)\, \) - vilket vi redan gjorde i förra paragraf - och sedan beräkna \( \,g(x)\):s värde för \( x = -3\, \):

\[ g(-3) = {2 \cdot (-3) \over -3 - 3} = {-6 \over -6} = 1 \]

Värdet \( 1\, \) överensstämmer med \( \,f(x)\):s gränsvärde när \( x\, \) närmar sig \( -3\, \). Dvs \( f(x)\, \) går mot \( 1\, \) när \( x\, \) går mot \( -3\, \) både från vänster och höger.

Då är det möjligt att definiera den nya funktionen \( g(x)\, \) som en lite modifierad version av \( \,f(x)\). Modifikationen består i att lägga till värdet \( 1\, \) i den nya funktionen för \( x = -3\, \) så att den blir både definierad och kontinuerlig för \( x = -3\, \). För alla andra \( x\, \) är den identisk med \( f(x)\, \). Så här kan man definiera den nya funktionen \( g(x)\, \):

\[ g(x) \, = \, \begin{cases} \displaystyle {2\,x^2 + 6\,x \over x^2 - 9} & \mbox{om } x \neq -3 \\ \\ 1 & \mbox{om } x = -3 \end{cases}\]

Denna definition är uppdelad i två olika fall: För alla \( x \neq -3\, \) definieras funktionen \( g(x)\, \) enligt det rationella uttrycket för \( f(x)\, \), medan för \( x = -3\, \) har den värdet \( 1\, \). \( g(x)\, \) är den kontinuerliga fortsättningen av \( f(x)\, \). Den är lämpligare att användas istället för \( f(x)\, \) eftersom man hat lyckats att eliminera åtminstone den hävbara diskontinuiteten.

Självklart är denna nya definition helt och hållet identisk med den förenklade form som vi hade fått tidigare:

\[ g(x) = {2 \, x \over x - 3} \]

I beräkningssammanhang och när man ritar grafen föredrar man förstås denna enkla form. Nackdelen med en är bara att den inte längre innehåller ens ett spår av den ursprungliga funktionen \( f(x)\, \). Man ser inte direkt att den är en kontinuerlig fortsättning av \( f(x)\, \).

Den andra faktorn \( (x-3)\, \) både i \( \,f(x)\):s och \( \,g(x)\):s nämnare som inte kan förkortas ger upphov till den andra diskontinuiteten av dessa två funktioner i \( x = 3\, \). Denna diskontinuitet är dock inte hävbar. När \( x\, \) går mot \( 3\, \) går \( f(x)\, \) inte mot ett ändligt värde utan mot oändligheten. Därför är diskontinuiteten i \( x = 3\, \) kvar och synlig i graferna till både \( f(x)\, \) och \( g(x)\, \). Den är, till skillnad från den första, en icke-hävbar diskontinuitet och kan inte repareras på något sätt. Denna "allvarliga" diskontinuitet finns även kvar i den kontinuerliga fortsättningen \( g(x)\, \) och är inte hävbar där heller. Så \( g(x)\, \) har en diskontinuitet kvar medan \( f(x)\, \) hade två diskontinuiteter.

Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.