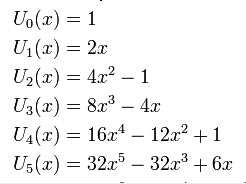1.1 Polynom

Innehåll

1 Vad är ett polynom?
2 Ett polynoms grad
3 Ett polynoms värde
4 Addition och subtraktion av polynom
5 Multiplikation av polynom
6 Internetlänkar

Vad är ett polynom?

Ordet "poly" betyder på latin många och "nom" som egentligen betyder namn, har i matematiken innebörden term. Så "polynom" betyder många termer. Närmare bestämt är ett polynom en summa av många termer. Men vad exakt är en term och hur ser den ut? När man pratar om polynom menar man med term ett uttryck av formen:

\[ a \cdot x^n \]

där n är ett positivt heltal eller 0. Dvs n får varken vara negativt eller ett bråk (decimaltal). Talet a kallas kofficient och är en godtycklig men fast konstant. x däremot är en variabel som kan anta vilka värden som helst. Ett exempel på en term är:

\[ -8 \cdot x^3 \]

Om ett polynom ska vara en summa av många sådana termer då måste polynom vara en speciell form av ett uttryck. Och tilldelar man det till ett y då blir det en speciell form av en funktion, därför att varje term innehåller variabeln x. Samma sak gäller förstås för en summa av termer. Polynom är faktiskt en typ av funktioner, närmare bestämt en generalisering samt utvidgning av de funktioner vi sysslat hittills med. I Matte A-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ\[ y = 4\,x + 12 \]

Här förekommer \( x \) högst som 1:a gradspotens dvs med exponenten 1. Grafen är en rät linje. I Matte B-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ\[ y = 3\,x^2 + 5\,x - 16 \]

Här är den högsta exponenten till \( x \) 2. Grafen är en parabel. Redan dessa funktioner är polynom utan att vi kallade dem så, därför att de är summor av termer som uppfyller de villkor som vi införde för n - nämligen att vara ett positivt heltal eller 0. Om du har det svårt att se varför även konstanterna 12 och -16 i exemplen ovan kan anses som "termer" i den inledningsvis definierade bemärkelsen, kom ihåg att man kan skriva 12 som:

\[ 12 \cdot x^0 \]

Att man kan göra så beror på att enligt potenslagarna \( x^0 \) är lika med 1. Samma sak gäller för -16 som också är en term därför att -16 är lika med \( -16\,x^0 \). Därmed har vi identifierat både \( 4\,x + 12 \) och \( 3\,x^2 + 5\,x - 16 \) som polynom.

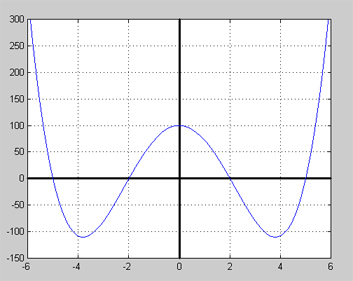
I Matte C-kursen ska vi nu lära oss att hantera även polynom av högre grad än 2 som t.ex.\[ y = x^4 - 29\;x^2 + 100 \] vars graf ser ut så här:

Som man ser är grafen mer komplicerad än parabeln. Framför allt har den mer minima och maxima och mer nollställen som inte av en tillfällighet är identiska med lösningarna till 4:e gradsekvationen \( x^4 - 29\;x^2 = -100 \) i övning 6 (förra avsnitt 1.1 Ekvationer). Det känns naturligt att kalla polynomet \( x^4 - 29\;x^2 + 100 \) för ett 4:e gradspolynom, vilket leder oss till det allmänna begreppet grad av ett polynom.

Ett polynoms grad

Den högst förekommande x-potensen i ett polynom dvs den största exponenten till x bland polynomets alla termer kallas polynomets grad. Den term som innehåller denna högsta x-potens kallas polynomets ledande term.

I exemplet ovan har polynomet

\( x^4 - 29\;x^2 + 100 \)

graden 4 eftersom den högst förekommande x-potensen har exponenten 4. Den ledande termen är \( x^4 \).

Generellt har ett polynom av graden n följande form:

\[ a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad . . . \quad + a_1 \cdot x + a_0 \]

Den ledande termen är \( a_n \cdot x^n \) och den konstanta termen är \( a_0 \). Även om det ur ren beräkningssynpunkt är helt irrelevant i vilken ordning man skriver ett polynoms termer, brukar man ändå börja med den ledande termen, skriva termerna i avatagende exponentordning och avsluta med den konstanta termen.

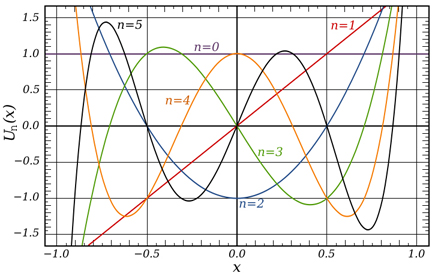
Ett polynoms grad är ett mått på dess kompexitet. Ett exempel på hur kompexiteten växer med graden är följande sex polynom vars grafer är ritade i samma koordinatsystem: