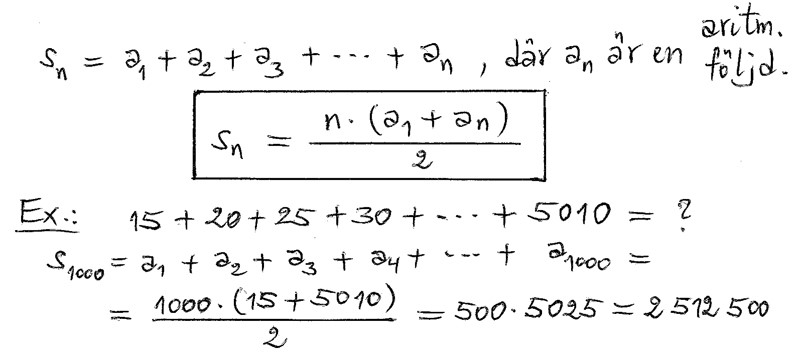Aritmetisk summa = Summan av en aritmetisk talföljd

Summatecknet \( \; \sum \; \)

Den stora bokstaven Sigma i det grekiska alfabetet används i matematiken som symbol för summa.

Man gör det för att kunna skriva långa summor på ett kompakt sätt.

T.ex. skulle rutan ovan \(-\) skriven med summatecknet \(-\) inledas så här:

\( \quad s_n \, = \, \displaystyle\sum_{k=1}^{n} a_k \; \), där \( \; a_n \; \) är en aritmetisk följd. \( \quad \)

Summatecknet läses\[ \qquad \] "Summa \(a_k\), då \(k\) går från \(1\) till \(n\)".

\(a_k\) kallas summand, \(1\) det första och \(n\) det sista indexet.

\(k\) kallas indexvariabeln och kan bytas ut mot vilken annan bokstav som helst.

Eller istället för att skriva den långa summan

\(1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20\)

kan man skriva \( \quad \displaystyle\sum_{k=1}^{20} k = 1 + 2 + 3 + \ldots + 19 + 20\).

Vill man skriva summan av alla heltal från och med 7 till och med 23 skriver man:

\[\sum_{k=7}^{23} k = 7 + 8 + 9 + \ldots + 22 + 23\].

Vill man summera t.ex. kvadraterna av alla tal från 1 till 5 skriver man:

\[\sum_{k=1}^5 k^2 = 1 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55\].