3.2 Lösning 1a
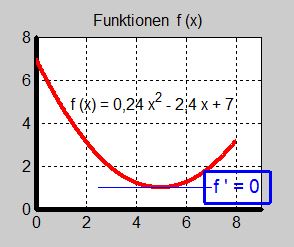
a) \( f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \)
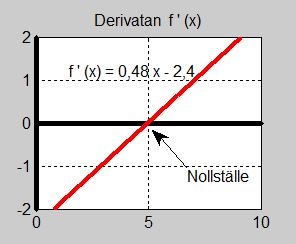
- \[ f'(x) \, = \, 0,48\,x - 2,4 \]
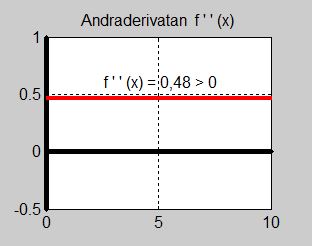
- \[ f''(x) \, = \, 0,48 \]
b) För att få reda på derivatans nollställe som reglerna om maxima och minima med andraderivata kräver sätter vi derivatan till \( \, 0 \) och beräknar tidpunkten \( x \, \) då derivatan blir \( \, 0 \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Nu vet vi att derivatan blir \( \, 0 \) i \( x = 5 \, \) dvs tangenten till kurvan \( y = f(x) \, \) har lutningen \( 0\, \) dvs är horisontell i \( x = 5 \, \). Men en horisontell tangent kan vara ett maximum eller ett minimum.
För att avgöra om det föreligger ett maximum eller ett minimum kräver regeln andraderivatans tecken. Därför sätter vi \( x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ f''(5) = 0,48 \,>\, 0 \]
Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( f(x) \, \) har ett minimum i \( x_{min} = 5 \, \).
Alltså är nattens kallaste tidpunkt kl \( 5 \, \).