Skillnad mellan versioner av "Huvudsida"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 26: | Rad 26: | ||
| − | <div class="ovnE"> | + | = <b><span style="color:#931136">Kursens beskrivning</span></b> = |
| + | <div class="ovnE"><big> | ||
<b>Matematik 5 </b> är en fortsättningskurs på Matematik 4 för gymnasiets Natur- och Teknikprogram. | <b>Matematik 5 </b> är en fortsättningskurs på Matematik 4 för gymnasiets Natur- och Teknikprogram. | ||
| + | |||
| + | Kursen följer Skolverkets [https://vidma.se/matematik-5-centralt-innehall-och-betygskriterier <b><span style="color:blue">kursplan</span></b>] och tillämpar Skolverkets betygskriterier. | ||
Den motsvarar delvis den kurs som i den gamla kursplanen hette Matematik E resp. Diskret matematik. | Den motsvarar delvis den kurs som i den gamla kursplanen hette Matematik E resp. Diskret matematik. | ||
| Rad 44: | Rad 47: | ||
För detaljerat upplägg se [[Matte 5 Innehållsförteckning|<b><span style="color:blue">innehållsförteckningen</span></b>]]. | För detaljerat upplägg se [[Matte 5 Innehållsförteckning|<b><span style="color:blue">innehållsförteckningen</span></b>]]. | ||
| − | </div> | + | </big></div> |
Versionen från 18 augusti 2024 kl. 18.04
| Innehållsförteckning | Kursens presentation | Centralt_innehåll_Ma5 | Formelsamling Matte 5 | Lektion 1 >> |

|
|
Kursens beskrivning
Matematik 5 är en fortsättningskurs på Matematik 4 för gymnasiets Natur- och Teknikprogram.
Kursen följer Skolverkets kursplan och tillämpar Skolverkets betygskriterier.
Den motsvarar delvis den kurs som i den gamla kursplanen hette Matematik E resp. Diskret matematik.
Kursen kan ge meritpoäng som frivillig kurs för gymnasiets andra program.
Den passar även för vuxenutbildningen.
Matematik 5 förutsätter förkunskaper från kurser motsvarande Matematik 4, även om inte i alla delar.
Kursen börjar med talteori och bevismetoder, fortsätter med en kort genomgång av klassisk mängdlära som
kan vara till hjälp för förståelsen av kombinatorik som sedan följer.
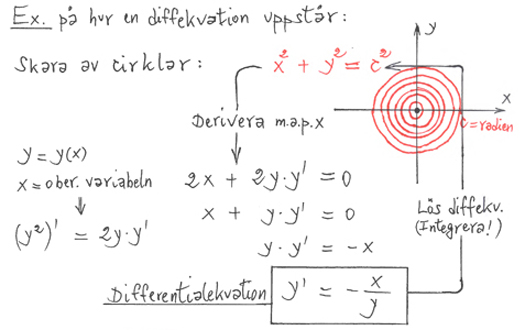
Matematik 5 avslutas med differentialekvtioner och ett urval av tillämpade matematiska problem (Problemlösning).
För detaljerat upplägg se innehållsförteckningen.
Copyright © 2024 Lieta AB. All Rights Reserved.