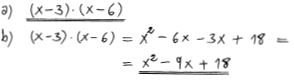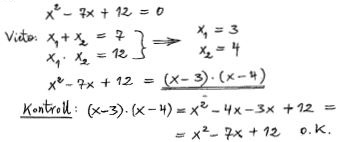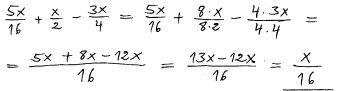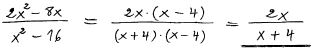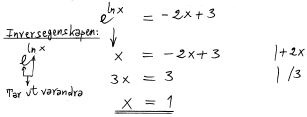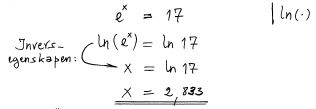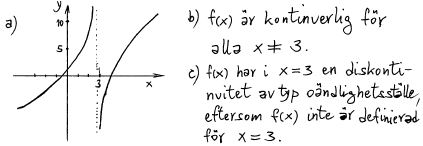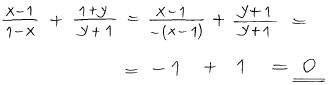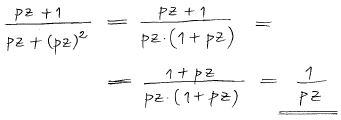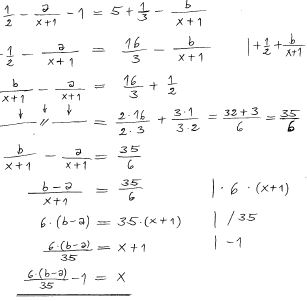Skillnad mellan versioner av "Lösningar till diagnosprov 1 kap 1"

Från Mathonline
Hoppa till: navigering, sök
m
m
Rad 10: Rad 10:
 
|}
 
|}
  
−
[[Image: Losningar diagnos 1 Ma3_1_Sid_1_20b.jpg]]
 
−
[[Image: Losningar diagnos 1 Ma3_1_Sid_2_20b.jpg]]
 
−
[[Image: Losningar diagnos 1 Ma3_1_Sid_3_25.jpg]]
 
−
[[Image: Losningar diagnos 1 Ma3c1-sid4_20.jpg]]
 
−
[[Image: Losningar diagnos 1 Ma3c1 Sida 5_20.jpg]]
 
−
[[Image: Losningar diagnos 1 Ma3c1 Sida 6_20.jpg]]
 
  
 +
== Uppgift 1 ==
 +
a) &nbsp; Ange ett polynom i faktorform vars nollställen är <math> \, 3 \, </math> och <math> \, 6 \, </math>.
  
 +
b) &nbsp; Utveckla faktorformen från a) till ett polynom som en summa av termer.
  
−
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved.
+
<u>Lösning:</u>
 +
 
 +
:::[[Image: Losg_diagnos_1_1_1_40.jpg]]
 +
 
 +
== Uppgift 2 ==
 +
Faktorisera följande polynom<span style="color:black">:</span> <math> \qquad {x^{2}}\; - \; 7 \; x \, \; + \; \,12 \, </math>
 +
 
 +
Kontrollera din lösning.
 +
 
 +
<u>Lösning:</u>
 +
 
 +
::[[Image: Losg_diagnos_1_1_2_50.jpg]]
 +
 
 +
== Uppgift 3 ==
 +
Följande uttryck är givet<span style="color:black">:</span> <math> \qquad P(x) \; = \; 4\;{x^{3}}\; - \;\,2\;{x^2}\,(2\;x + \; \,6)\;\, + \;\,7\;x\,\,(3\; + \;2\;x) \, </math>
 +
 
 +
a) &nbsp; Utveckla <math> \; P(x) \; </math>  till ett polynom. Ange polynomets koefficienter och grad.
 +
 
 +
b) &nbsp; Använd polynomet från a) för att beräkna <math> \; P(-1) </math>.
 +
 
 +
c) &nbsp; Bestäm alla nollställen till  polynomet från a).
 +
 
 +
d) &nbsp; Faktorisera polynomet <math> \; P(x) </math>. Kontrollera din lösning.
 +
 
 +
<u>Lösning:</u>
 +
::[[Image: Losg_diagnos_1_1_3_55.jpg]]
 +
 
 +
 
 +
== Uppgift 4 ==
 +
Förenkla så långt som möjligt<span style="color:black">:</span> <math> \qquad \displaystyle {5\,x \over 16} \, + \, {x \over 2} \, - \, {3\,x \over 4} </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_4_50.jpg]]
 +
 
 +
== Uppgift 5 ==
 +
Förenkla det rationella uttrycket<span style="color:black">:</span> <math> \qquad \displaystyle \frac{{2\;{x^2}\; - \;8\;x}}{{{x^2}\; - \;16}} </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_5_50.jpg]]
 +
 
 +
== Uppgift 6 ==
 +
Lös ekvationen exakt<span style="color:black">:</span> <math> \qquad\quad {e^{\;\ln  x}}\; = \; - 2x + 3 </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_6_40.jpg]]
 +
 
 +
== Uppgift 7 ==
 +
Lös ekvationen<span style="color:black">:</span> <math> \qquad\qquad\qquad {e^{\;x}} = 17 </math>
 +
 
 +
Ange svaret med tre decimaler.
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_7_40.jpg]]
 +
 
 +
== Uppgift 8 ==
 +
Följande funktion är given<span style="color:black">:</span> <math> \qquad\qquad \displaystyle f(x) \, = \, {x^2 - 3x - 4 \over x - 3} \, </math>
 +
 
 +
a) &nbsp; Rita grafen till <math> \, f(x) </math>.
 +
 
 +
b) &nbsp; För vilka <math> \, x \, </math> är <math> \, f(x) \, </math> kontinuerlig och för vilka är den inte kontinuerlig?
 +
 
 +
c) &nbsp; Ange de förekommande diskontinuiteternas typ. Motivera dina svar.
 +
 
 +
<u>Lösning:</u>
 +
 
 +
[[Image: Losg_diagnos_1_1_8_50.jpg]]
 +
 
 +
== Uppgift 9 ==
 +
Lös ekvationen algebraiskt<span style="color:black">:</span> <math> \qquad\qquad \left| {x + 1} \right|\;\, + \;\,2\,x\;\, = \,\;3 </math>
 +
 
 +
<u>Lösning:</u>
 +
 
 +
<b>Fall 1:</b> <math> {\color{White} x} x + 1 \geq 0 \quad {\color{White} x} </math> eller <math> {\color{White} x}\quad x \geq -1 </math>
 +
 
 +
Enligt absolutbeloppets definition blir i så fall <math> | \, x + 1 \, | = x + 1\, </math> och ekvationen blir:
 +
 
 +
::<math>\begin{align}  x + 1 + 2\,x & = 3      \\
 +
                          3\,x + 1 & = 3      \\
 +
                              3\,x & = 3 - 1  \\
 +
                              3\,x & = 2      \\
 +
                              x_1  & = {2 \over 3}
 +
        \end{align}</math>
 +
 
 +
Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i detta fall, nämligen <math> x \geq -1 </math>.
 +
 
 +
Det stämmer att <math> \displaystyle {2 \over 3} \geq -1 </math>. Därmed kan vi godta lösningen <math> \displaystyle x_1  = {2 \over 3} </math>.
 +
 
 +
<b>Fall 2:</b> <math> {\color{White} x} x + 1 < 0 \quad {\color{White} x} </math> eller <math> {\color{White} x}\quad x < -1 </math>
 +
 
 +
Enligt absolutbeloppets definition blir i så fall <math> | \, x + 1 \, | = -(x + 1) = -x - 1\, </math> och ekvationen blir:
 +
 
 +
::<math>\begin{align}  -\,x -1 + 2\,x & = 3    \\
 +
                                x - 1 & = 3    \\
 +
                                  x_2 & = 4
 +
        \end{align}</math> 
 +
 
 +
Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i detta fall, nämligen <math> x < -1 </math>.
 +
 
 +
Faktiskt är <math> 4 \not< -1 </math> utan det gäller <math> 4 > -1 </math>. Därmed måste vi förkasta lösningen <math> x_2  = 4 </math> som är en falsk rot.
 +
 
 +
Ekvationen har endast lösningen:
 +
 
 +
::::<math> x = {2 \over 3} </math>
 +
 
 +
== Uppgift 10 ==
 +
Lös följande ekvation exakt<span style="color:black">:</span> <math> \;\; \ln x = 1 + \ln \,(x - 1) </math>
 +
 
 +
<u>Lösning:</u>
 +
 
 +
:::::<math>\begin{align} \ln\,x                          & = 1 + \ln\,(x-1)  \; & &\;| \; - \ln\,(x-1) \\
 +
                    \ln\,x - \ln\,(x-1)            & = 1 \; & &: \;\text{Logaritmlag 2 i VL}    \\
 +
                    \ln\,\left({x \over x-1}\right) & = 1 \; & &\;| \; e\,^{\cdot}  \\
 +
                                      {x \over x-1} & = e \; & &\;| \; \cdot (x-1)  \\
 +
                                                  x & = e \cdot (x-1)                        \\
 +
                                                  x & = e \cdot x - e \;  & &\;| \; + e - x    \\
 +
                                                  e & = e \cdot x - x \;  & &: \;\text{Bryt ut} \; x \;\text{i HL } \\
 +
                                                  e & = x \cdot (e - 1) \; & &\;| \; / \; (e-1) \\
 +
                                                  x & = {e \over e-1}
 +
      \end{align}</math>
 +
 
 +
== Uppgift 11 ==
 +
Förenkla så långt som möjligt<span style="color:black">:</span> <math> \qquad \displaystyle {x \, - \, 1 \over 1\, - \,x} \; + \; {1\, + \,y \over y\, + \, 1} </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_11_50.jpg]]
 +
 
 +
== Uppgift 12 ==
 +
Förenkla det rationella uttrycket<span style="color:black">:</span> <math> \qquad \displaystyle {{p\,z \, + \, 1} \over {p\,z \, + \, (p\,z)\,^2}} </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_12_50.jpg]]
 +
 
 +
== Uppgift 13==
 +
Lös ut <math> \, x \, </math> från<span style="color:black">:</span> <math> \qquad \displaystyle{\frac{1}{2} - \frac{a}{x + 1} - 1 = 5 + \frac{1}{3} - \frac{b}{x + 1}} </math>
 +
 
 +
<u>Lösning:</u>
 +
:::[[Image: Losg_diagnos_1_1_13_40.jpg]]
 +
 
 +
 
 +
== Uppgift 14 ==
 +
På ett bankkonto har ett kapital på <math> \, 100\,000 \, </math> kr under <math> \, 5 \, </math> år vuxit till <math> \, 190\,000\, </math> kr.
 +
 
 +
a) &nbsp; Vilken räntesats per år hade kontot? Ange svaret med en decimal.
 +
 
 +
b) &nbsp; Vilken typ av ekvation blir det i a) och vilken operation löser ekvationen?
 +
 
 +
c) &nbsp; Använd räntesatsen från a) för att besvara frågan:
 +
 
 +
:Hur länge tar det tills startkapitalet tredubblats?
 +
 
 +
:Avrunda svaret till hela år och månader.
 +
 
 +
d) &nbsp; Vilken typ av ekvation blir det i c) och vilken operation löser ekvationen?
 +
 
 +
<u>Lösning:</u>
 +
 
 +
:[[Image: Losg_diagnos_1_1_14_40.jpg]]
 +
 
 +
 
 +
== Uppgift 15 ==
 +
Bakterier i mjölk anses växa enligt modellen:
 +
 
 +
:::::<math> \, y =  10 \cdot  e{\,^{0,5\,x}} </math>
 +
               
 +
där <math> \, y \, </math> är antalet bakterier och <math> \, x \, </math> tiden i timmar.
 +
 
 +
a) &nbsp; Hur många bakterier finns det i mjölken i början?
 +
 
 +
b) &nbsp; Hur många bakterier kommer det att finnas i mjölken efter <math> \, 8 \, </math> timmar?
 +
 
 +
c) &nbsp; Efter hur många timmar och minuter blir mjölken sur?
 +
 
 +
:Mjölken anses vara sur när antalet bakterier har uppnått <math> \, 1\,250 </math>.
 +
 
 +
<u>Lösning:</u>
 +
 
 +
:[[Image: Losg_diagnos_1_1_15_40.jpg]]
 +
 
 +
 
 +
<!-- [[Image: Losningar diagnos 1 Ma3_1_Sid_1_20b.jpg]] -->
 +
<!-- [[Image: Losningar diagnos 1 Ma3_1_Sid_2_20b.jpg]] -->
 +
<!-- [[Image: Losningar diagnos 1 Ma3_1_Sid_3_25.jpg]] -->
 +
<!-- [[Image: Losningar diagnos 1 Ma3c1-sid4_20.jpg]] -->
 +
<!-- [[Image: Losningar diagnos 1 Ma3c1 Sida 5_20.jpg]] -->
 +
<!-- [[Image: Losningar diagnos 1 Ma3c1 Sida 6_20.jpg]] -->
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[[Matte:Copyrights|Copyright]] © 2011-2015 Math Online Sweden AB. All Rights Reserved.

Versionen från 30 april 2015 kl. 14.45

       Diagnosprov 1 kap 1          Lösningar till diagnos 1 (PDF)          Innehållsförteckning kap 1          Diagnosprov 2 kap 1          Lösningar till diagnosprov 2 kap 1      


Uppgift 1

a)   Ange ett polynom i faktorform vars nollställen är \( \, 3 \, \) och \( \, 6 \, \).

b)   Utveckla faktorformen från a) till ett polynom som en summa av termer.

Lösning:

Losg diagnos 1 1 1 40.jpg

Uppgift 2

Faktorisera följande polynom: \( \qquad {x^{2}}\; - \; 7 \; x \, \; + \; \,12 \, \)

Kontrollera din lösning.

Lösning:

Losg diagnos 1 1 2 50.jpg

Uppgift 3

Följande uttryck är givet: \( \qquad P(x) \; = \; 4\;{x^{3}}\; - \;\,2\;{x^2}\,(2\;x + \; \,6)\;\, + \;\,7\;x\,\,(3\; + \;2\;x) \, \)

a)   Utveckla \( \; P(x) \; \) till ett polynom. Ange polynomets koefficienter och grad.

b)   Använd polynomet från a) för att beräkna \( \; P(-1) \).

c)   Bestäm alla nollställen till polynomet från a).

d)   Faktorisera polynomet \( \; P(x) \). Kontrollera din lösning.

Lösning:

Losg diagnos 1 1 3 55.jpg


Uppgift 4

Förenkla så långt som möjligt: \( \qquad \displaystyle {5\,x \over 16} \, + \, {x \over 2} \, - \, {3\,x \over 4} \)

Lösning:

Losg diagnos 1 1 4 50.jpg

Uppgift 5

Förenkla det rationella uttrycket: \( \qquad \displaystyle \frac{{2\;{x^2}\; - \;8\;x}}{{{x^2}\; - \;16}} \)

Lösning:

Losg diagnos 1 1 5 50.jpg

Uppgift 6

Lös ekvationen exakt: \( \qquad\quad {e^{\;\ln x}}\; = \; - 2x + 3 \)

Lösning:

Losg diagnos 1 1 6 40.jpg

Uppgift 7

Lös ekvationen: \( \qquad\qquad\qquad {e^{\;x}} = 17 \)

Ange svaret med tre decimaler.

Lösning:

Losg diagnos 1 1 7 40.jpg

Uppgift 8

Följande funktion är given: \( \qquad\qquad \displaystyle f(x) \, = \, {x^2 - 3x - 4 \over x - 3} \, \)

a)   Rita grafen till \( \, f(x) \).

b)   För vilka \( \, x \, \) är \( \, f(x) \, \) kontinuerlig och för vilka är den inte kontinuerlig?

c)   Ange de förekommande diskontinuiteternas typ. Motivera dina svar.

Lösning:

Losg diagnos 1 1 8 50.jpg

Uppgift 9

Lös ekvationen algebraiskt: \( \qquad\qquad \left| {x + 1} \right|\;\, + \;\,2\,x\;\, = \,\;3 \)

Lösning:

Fall 1: \( {\color{White} x} x + 1 \geq 0 \quad {\color{White} x} \) eller \( {\color{White} x}\quad x \geq -1 \)

Enligt absolutbeloppets definition blir i så fall \( | \, x + 1 \, | = x + 1\, \) och ekvationen blir:

\[\begin{align} x + 1 + 2\,x & = 3 \\ 3\,x + 1 & = 3 \\ 3\,x & = 3 - 1 \\ 3\,x & = 2 \\ x_1 & = {2 \over 3} \end{align}\]

Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i detta fall, nämligen \( x \geq -1 \).

Det stämmer att \( \displaystyle {2 \over 3} \geq -1 \). Därmed kan vi godta lösningen \( \displaystyle x_1 = {2 \over 3} \).

Fall 2: \( {\color{White} x} x + 1 < 0 \quad {\color{White} x} \) eller \( {\color{White} x}\quad x < -1 \)

Enligt absolutbeloppets definition blir i så fall \( | \, x + 1 \, | = -(x + 1) = -x - 1\, \) och ekvationen blir:

\[\begin{align} -\,x -1 + 2\,x & = 3 \\ x - 1 & = 3 \\ x_2 & = 4 \end{align}\]

Vi kollar om lösningen inte står i motsats till förutsättningen vi gjorde i detta fall, nämligen \( x < -1 \).

Faktiskt är \( 4 \not< -1 \) utan det gäller \( 4 > -1 \). Därmed måste vi förkasta lösningen \( x_2 = 4 \) som är en falsk rot.

Ekvationen har endast lösningen:

\[ x = {2 \over 3} \]

Uppgift 10

Lös följande ekvation exakt: \( \;\; \ln x = 1 + \ln \,(x - 1) \)

Lösning:

\[\begin{align} \ln\,x & = 1 + \ln\,(x-1) \; & &\;| \; - \ln\,(x-1) \\ \ln\,x - \ln\,(x-1) & = 1 \; & &: \;\text{Logaritmlag 2 i VL} \\ \ln\,\left({x \over x-1}\right) & = 1 \; & &\;| \; e\,^{\cdot} \\ {x \over x-1} & = e \; & &\;| \; \cdot (x-1) \\ x & = e \cdot (x-1) \\ x & = e \cdot x - e \; & &\;| \; + e - x \\ e & = e \cdot x - x \; & &: \;\text{Bryt ut} \; x \;\text{i HL } \\ e & = x \cdot (e - 1) \; & &\;| \; / \; (e-1) \\ x & = {e \over e-1} \end{align}\]

Uppgift 11

Förenkla så långt som möjligt: \( \qquad \displaystyle {x \, - \, 1 \over 1\, - \,x} \; + \; {1\, + \,y \over y\, + \, 1} \)

Lösning:

Losg diagnos 1 1 11 50.jpg

Uppgift 12

Förenkla det rationella uttrycket: \( \qquad \displaystyle {{p\,z \, + \, 1} \over {p\,z \, + \, (p\,z)\,^2}} \)

Lösning:

Losg diagnos 1 1 12 50.jpg

Uppgift 13

Lös ut \( \, x \, \) från: \( \qquad \displaystyle{\frac{1}{2} - \frac{a}{x + 1} - 1 = 5 + \frac{1}{3} - \frac{b}{x + 1}} \)

Lösning:

Losg diagnos 1 1 13 40.jpg


Uppgift 14

På ett bankkonto har ett kapital på \( \, 100\,000 \, \) kr under \( \, 5 \, \) år vuxit till \( \, 190\,000\, \) kr.

a)   Vilken räntesats per år hade kontot? Ange svaret med en decimal.

b)   Vilken typ av ekvation blir det i a) och vilken operation löser ekvationen?

c)   Använd räntesatsen från a) för att besvara frågan:

Hur länge tar det tills startkapitalet tredubblats?
Avrunda svaret till hela år och månader.

d)   Vilken typ av ekvation blir det i c) och vilken operation löser ekvationen?

Lösning:

Losg diagnos 1 1 14 40.jpg


Uppgift 15

Bakterier i mjölk anses växa enligt modellen:

\[ \, y = 10 \cdot e{\,^{0,5\,x}} \]

där \( \, y \, \) är antalet bakterier och \( \, x \, \) tiden i timmar.

a)   Hur många bakterier finns det i mjölken i början?

b)   Hur många bakterier kommer det att finnas i mjölken efter \( \, 8 \, \) timmar?

c)   Efter hur många timmar och minuter blir mjölken sur?

Mjölken anses vara sur när antalet bakterier har uppnått \( \, 1\,250 \).

Lösning:

Losg diagnos 1 1 15 40.jpg






Copyright © 2011-2015 Math Online Sweden AB. All Rights Reserved.

Hämtad från "https://matte5.mathonline.se/index.php?title=Lösningar_till_diagnosprov_1_kap_1&oldid=22219"