Skillnad mellan versioner av "Huvudsida"

Versionen från 23 juni 2024 kl. 13.42

Välkommen till

Matematik 5

i Math Online \(-\) ett webbaserat digitalt läromedel för matematik

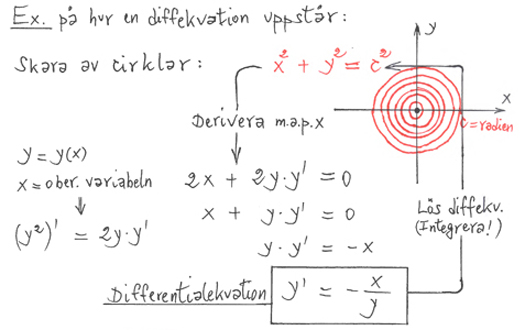
Matematik 5 är en fortsättningskurs på Matematik 4 för gymnasiets Natur- och Teknikprogram.

Den motsvarar delvis den kurs som i den gamla kursplanen hette Matematik E resp. Diskret matematik.

Kursen kan ge meritpoäng som frivillig kurs för gymnasiets Naturvetenskaps-, Teknik-, Samhällsvetenskaps-,

Ekonomi- och andra program. Den passar även för vuxenutbildningen.

Matematik 5 förutsätter förkunskaper från kurser motsvarande Matematik 4, även om inte i alla delar.

Kursen börjar med talteori och bevismetoder, fortsätter med en kort genomgång av klassisk mängdlära som

kan vara till hjälp för förståelsen av kombinatorik som sedan följer.

Matematik 5 avslutas med differentialekvtioner och ett urval av matematiska problem ur tillämpningarna (Problemlösning).

För detaljerat upplägg se innehållsförteckningen.

@@ Rad 34: / Rad 34: @@
 Matematik 5 förutsätter förkunskaper från kurser motsvarande Matematik 4, även om inte i alla delar.
-Kursen börjar med talteori och bevismetoder, fortsätter med en kort genomgång av klassisk mängdlära som kan vara till hjälp för förståelsen av kombinatorik som edan följer.
+Kursen börjar med talteori och bevismetoder, fortsätter med en kort genomgång av klassisk mängdlära som
-Matematik 5 avslutas med differentialekvtioner och ett urval av matematiska problem ur tillämpningarna. För detaljerat upplägg se [[Matte 5 Innehållsförteckning|<b><span style="color:blue">innehållsförteckningen</span></b>]].
+kan vara till hjälp för förståelsen av kombinatorik som sedan följer.
+Matematik 5 avslutas med differentialekvtioner och ett urval av matematiska problem ur tillämpningarna (Problemlösning).
+För detaljerat upplägg se [[Matte 5 Innehållsförteckning|<b><span style="color:blue">innehållsförteckningen</span></b>]].
 </div>