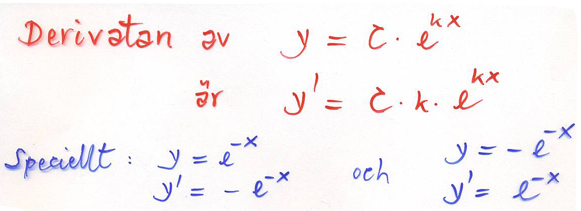Skillnad mellan versioner av "2.6 Derivatan av exponentialfunktioner"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 28: | Rad 28: | ||
Svaret är: Ja, om och endast om <math> {\color{White} x} a \, = \, e </math> . Detta är möjligt eftersom vi har friheten att välja en bas. | Svaret är: Ja, om och endast om <math> {\color{White} x} a \, = \, e </math> . Detta är möjligt eftersom vi har friheten att välja en bas. | ||
| − | Man vänder alltså på steken: Istället för att fråga efter deriveringsregeln, ger man en deriveringsregel <math>-</math> den enklaste möjliga, nämligen <strong><span style="color:red">derivatan = funktionen</span></strong> <math>-</math> och frågar efter en <strong><span style="color:red">bas</span></strong> som uppfyller | + | Man vänder alltså på steken: Istället för att fråga efter deriveringsregeln, ger man en deriveringsregel <math>-</math> den enklaste möjliga, nämligen <strong><span style="color:red">derivatan = funktionen</span></strong> <math>-</math> och frågar efter en <strong><span style="color:red">bas</span></strong> som uppfyller denna deriveringsregel. |
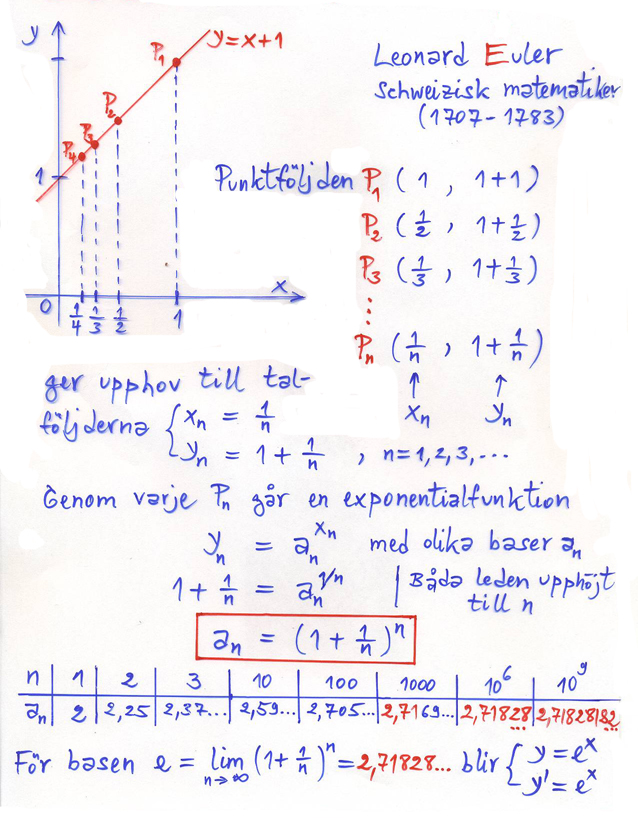
Frågeställningen har i matematikens historia motiverat den schweiziske matematikern [http://sv.wikipedia.org/wiki/Leonhard_Euler Leonard Euler] att ställa upp sin berömda formel för beräkning av talet <math> e\, </math> som vi använde i [[1.4_Talet_e:_Exponentialfunktionen_med_basen_e_och_den_naturliga_logaritmen#Hur_kom.28mer.29_talet_.5C.28_e_.5C.2C.5C.29_till.3F|<strong><span style="color:blue">Hur kom(mer) talet <big><math> e \,</math></big> till?</span></strong>]] för att beräkna <math> e\, </math>. På 1700-talet bevisade Euler att den efterfrågade basen var just <math> e\, </math>, varför talet kallats efter honom. Vi försöker nu att följa hans bevis. | Frågeställningen har i matematikens historia motiverat den schweiziske matematikern [http://sv.wikipedia.org/wiki/Leonhard_Euler Leonard Euler] att ställa upp sin berömda formel för beräkning av talet <math> e\, </math> som vi använde i [[1.4_Talet_e:_Exponentialfunktionen_med_basen_e_och_den_naturliga_logaritmen#Hur_kom.28mer.29_talet_.5C.28_e_.5C.2C.5C.29_till.3F|<strong><span style="color:blue">Hur kom(mer) talet <big><math> e \,</math></big> till?</span></strong>]] för att beräkna <math> e\, </math>. På 1700-talet bevisade Euler att den efterfrågade basen var just <math> e\, </math>, varför talet kallats efter honom. Vi försöker nu att följa hans bevis. | ||
Versionen från 23 oktober 2014 kl. 11.34
| <-- Förra avsnitt | Teori | Övningar | Nästa avsnitt --> |
Lektion 21 Derivatan av exponentialfunktioner
Innehåll
Derivatan av exponentialfunktionen \( y = e\,^x \)
Det kan vara bra att friska upp sina kunskaper om exponentialfunktionen med basen \( e\, \) (Eulers tal) från kapitel 1. Vi behöver nämligen i detta avsnitt att härleda derivatan av exponentialfunktionen \( y = e\,^x \) med basen \( e\, \) för att sedan kunna med hjälp av den ställa upp deriveringsregeln för den allmänna exponentialfunktionen \( y = a\,^x \) med en godtycklig bas \( a > 0\, \).
För att kunna göra det gör vi först ett försök med derivatans definition att ställa upp en deriveringsregel för \( y = a\,^x \). Försöket kommer att misslyckas, vilket kommer att leda oss till den avgörande frågeställning som kommer att lösa problemet. Denna frågeställning lyder:
Svaret är: Ja, om och endast om \( {\color{White} x} a \, = \, e \) . Detta är möjligt eftersom vi har friheten att välja en bas.
Man vänder alltså på steken: Istället för att fråga efter deriveringsregeln, ger man en deriveringsregel \(-\) den enklaste möjliga, nämligen derivatan = funktionen \(-\) och frågar efter en bas som uppfyller denna deriveringsregel.
Frågeställningen har i matematikens historia motiverat den schweiziske matematikern Leonard Euler att ställa upp sin berömda formel för beräkning av talet \( e\, \) som vi använde i Hur kom(mer) talet \( e \,\) till? för att beräkna \( e\, \). På 1700-talet bevisade Euler att den efterfrågade basen var just \( e\, \), varför talet kallats efter honom. Vi försöker nu att följa hans bevis.
Derivatan av den allmänna exponentialfunktionen \( y = a\,^x \)
Från att ha ställt upp deriveringsregeln för den naturliga exponentialfunktionen \( y = e\,^x \) är det bara ett enkelt steg till deriveringsregeln för den allmänna exponentialfunktionen \( y = a\,^x \) med en godtycklig bas \( a > 0\, \):
Specialfallet \( a = e\, \) och \( \ln a = \ln e = 1\, \) ger derveringsregeln \( y\,' = e^x \) för den naturliga exponentialfunktionen.
Uppdaterad tabell över deriveringsregler
I följande tabell är \( c,\,k,\,m,\,n,\,a \) konstanter, medan \( x\, \) och \( y\, \) är variabler, \( x\, \) den oberoende och \( y\, \) den beroende variabeln\[ y = f(x)\, \].
\( y\, \) \( y\,' \) \( c\, \) \( 0\, \) \( x\, \) \( 1\, \) \( a\; x \) \( a\, \) \( k\; x \, + \, m \) \( k\, \) \( x^2\, \) \( 2\,x \) \( a\,x^2 \) \( 2\,a\,x \) \( x^n\, \) \( n\cdot x\,^{n-1} \) \( a\,x\,^n \) \( n\cdot a\,x\,^{n-1} \) \( {1 \over x} \) \( - {1 \over x^2} \) \( \sqrt{x} \) \( {1 \over 2\, \sqrt{x}} \) \( e\,^x \) \( e\,^x \) \( e\,^{k\,x} \) \( k\cdot e\,^{k\,x} \) \( c\cdot e\,^{k\,x} \) \( c\cdot k\cdot e\,^{k\,x} \) \( a\,^x \) \( a\,^x \cdot \ln a \) \( f(x) + g(x)\, \) \( f\,'(x) + g\,'(x) \) \( a\cdot f(x) \) \( a\cdot f\,'(x) \)
De två sista raderna i tabellen är snarare generella satser än deriveringsregler. De gäller för alla funktioner \( f(x)\, \) och \( g(x)\, \). Av praktiska skäl tar vi upp dem ändå i samma tabell som deriveringsreglerna. Denna tabell kommer att ytterligare kompletteras i Matte 4-kursen då vi kommer att lära oss fler deriveringsregler och fler generella satser.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.