Skillnad mellan versioner av "Övningar till Ekvationer"
Taifun (Diskussion | bidrag) m (→Övning 1) |
Taifun (Diskussion | bidrag) m (→Övning 3) |
||
| (276 mellanliggande versioner av samma användare visas inte) | |||
| Rad 2: | Rad 2: | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[ | + | {{Not selected tab|[[Ekvationer|Teori]]}} |
| − | {{Selected tab|[[ | + | {{Selected tab|[[Övningar till Ekvationer|Övningar]]}} |
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | == | + | |
| + | == E-övningar: 1-3 == | ||
== Övning 1 == | == Övning 1 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande rotekvationer: | |
| + | |||
| + | a) <math> {\color{White} x} \sqrt{x} = 9 </math> | ||
| − | + | b) <math> {\color{White} x} \sqrt{x} = - 9 </math> | |
| − | + | c) <math> {\color{White} x} 5 - \sqrt{x} = 1 </math> | |
| − | </div>{{#NAVCONTENT:Svar 1a|1.1 Svar 1a|Lösning 1a|1.1 Lösning 1a|Svar 1b|1.1 Svar 1b|Lösning 1b|1.1 Lösning 1b}} | + | </div> {{#NAVCONTENT:Svar 1a|1.1 Svar 1a|Lösning 1a|1.1 Lösning 1a|Svar 1b|1.1 Svar 1b|Lösning 1b|1.1 Lösning 1b|Svar 1c|1.1 Svar 1c|Lösning 1c|1.1 Lösning 1c}} |
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 1a|Svar 1a]] | [[1.1 Lösning 1a|Lösning 1a]] | [[1.1 Svar 1b|Svar 1b]] | [[1.1 Lösning 1b|Lösning 1b]] | [[1.1 Svar 1c|Svar 1c]] | [[1.1 Lösning 1c|Lösning 1c]]</small></small> | ||
| + | --> | ||
== Övning 2 == | == Övning 2 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande ekvationer med den metod som förklaras i teoridelen. | |
| − | a) | + | a) <math> {\color{White} x} 2 \,\cdot \, \sqrt{x} - x = 1 </math> |
| − | b) | + | b) <math> {\color{White} x} x + \sqrt{5\,x - 1} = 3 </math> |
| − | </div>{{#NAVCONTENT:Svar 2a|1.1 Svar 2a|Lösning 2a|1.1 Lösning 2a|Svar 2b|1.1 Svar 2b|Lösning 2b|1.1 Lösning 2b}} | + | c) <math> {\color{White} x} 6\,x - 3\,\sqrt{9+x} = -9 </math> |
| + | |||
| + | </div> {{#NAVCONTENT:Svar 2a|1.1 Svar 2a|Lösning 2a|1.1 Lösning 2a|Svar 2b|1.1 Svar 2b|Lösning 2b|1.1 Lösning 2b|Svar 2c|1.1 Svar 2c|Lösning 2c|1.1 Lösning 2c}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 2a|Svar 2a]] | [[1.1 Lösning 2a|Lösning 2a]] | [[1.1 Svar 2b|Svar 2b]] | [[1.1 Lösning 2b|Lösning 2b]] | [[1.1 Svar 2c|Svar 2c]] | [[1.1 Lösning 2c|Lösning 2c]]</small></small> | ||
| + | --> | ||
== Övning 3 == | == Övning 3 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande rotekvationer: | |
| − | </div>{{#NAVCONTENT:Svar | + | a) <math> {\color{White} x} x = \sqrt{x+7} - 1 </math> |
| + | |||
| + | b) <big><math> {\color{White} x} {x + \sqrt{x} \over 7} </math></big> <math> = 6 </math> | ||
| + | |||
| + | c) <math> {\color{White} x} 2\,(x + 8) = 9\,\sqrt{4\,x} </math> | ||
| + | |||
| + | </div> {{#NAVCONTENT:Svar 3a|1.1 Svar 3a|Lösning 3a|1.1 Lösning 3a|Svar 3b|1.1 Svar 3b|Lösning 3b|1.1 Lösning 3b|Svar 3c|1.1 Svar 3c|Lösning 3c|1.1 Lösning 3c}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 3a|Svar 3a]] | [[1.1 Lösning 3a|Lösning 3a]] | [[1.1 Svar 3b|Svar 3b]] | [[1.1 Lösning 3b|Lösning 3b]] | [[1.1 Svar 3c|Svar 3c]] | [[1.1 Lösning 3c|Lösning 3c]]</small></small> | ||
| + | --> | ||
| + | |||
| + | == C-övningar: 4-8 == | ||
== Övning 4 == | == Övning 4 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös rotekvationen | |
| + | |||
| + | a) <math> \sqrt{x^2 + 1} = x - 3 </math> | ||
| + | |||
| + | b) Rita graferna till funktionerna <math> y_1 = \sqrt{x^2 + 1} </math> och <math> y_2 = x - 3\, </math> i ett och samma koordinatsystem. Använd följande inställningar för WINDOW i din grafritande räknare: Xmin = -10, Xmax = 10, Xscl = 2, Ymin = -10, Ymax = 10, Yscl = 2. Motivera ditt svar i a) med hjälp av graferna. | ||
| + | |||
| + | c) Rita graferna till funktionerna <math> \displaystyle y_1 = x^2 + 1 </math> och <math> y_2 = (x - 3)^2\, </math> i ett och samma koordinatsystem. Använd följande inställningar för WINDOW i din grafritande räknare: Xmin = -3, Xmax = 6, Xscl = 1, Ymin = 0, Ymax = 10, Yscl = 1. Tolka resultatet. | ||
| − | </div>{{#NAVCONTENT:Svar | + | </div>{{#NAVCONTENT:Svar 4a|1.1 Svar 4a|Lösning 4a|1.1 Lösning 4a|Lösning 4b|1.1 Lösning 4b|Lösning 4c|1.1 Lösning 4c}} |
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 4a|Svar 4a]] | [[1.1 Lösning 4a|Lösning 4a]] | [[1.1 Lösning 4b|Lösning 4b]] | [[1.1 Lösning 4c|Lösning 4c]]</small></small> | ||
| + | --> | ||
== Övning 5 == | == Övning 5 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | a) Modifiera rotekvationen | |
| − | </div>{{#NAVCONTENT:Svar | + | <math> \sqrt{x^2 + 1} = x - 3 </math> |
| + | |||
| + | i övning 4 så att den får en lösning genom att titta på grafen som du (förhoppningsvis) ritade i [[1.1 Lösning 4b|övning 4b]]. Rita graferna till funktionerna på bägge leden av den modifierade rotekvationen i ett och samma koordinatsystem så att man ser lösningen grafiskt. Använd samma inställningar för WINDOW i din grafritande räknare som i [[1.1 Lösning 4b|övning 4b]]. | ||
| + | |||
| + | b) Lös den modifierade rotekvationen algebraiskt. Ange svaret med 2 decimalers noggrannhet. | ||
| + | |||
| + | </div>{{#NAVCONTENT:Svar 5a|1.1 Svar 5a|Lösning 5a|1.1 Lösning 5a|Svar 5b|1.1 Svar 5b|Lösning 5b|1.1 Lösning 5b}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 5a|Svar 5a]] | [[1.1 Lösning 5a|Lösning 5a]] | [[1.1 Svar 5b|Svar 5b]] | [[1.1 Lösning 5b|Lösning 5b]]</small></small> | ||
| + | --> | ||
== Övning 6 == | == Övning 6 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös ekvationen | |
| + | |||
| + | <math> x^4 - 29\;x^2 = -100 </math> | ||
</div>{{#NAVCONTENT:Svar 6|1.1 Svar 6|Lösning 6|1.1 Lösning 6}} | </div>{{#NAVCONTENT:Svar 6|1.1 Svar 6|Lösning 6|1.1 Lösning 6}} | ||
| − | + | <!-- Alternativt: | |
| − | + | :<small><small>[[1.1 Svar 6|Svar 6]] | [[1.1 Lösning 6|Lösning 6]]</small></small> | |
| + | --> | ||
== Övning 7 == | == Övning 7 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande ekvation, som är samma som i övning 2a, här med substitutionen <math> t = \sqrt{x} </math>. | |
| + | |||
| + | <math> 2\,\sqrt{x} - x = 1 </math> | ||
</div>{{#NAVCONTENT:Svar 7|1.1 Svar 7|Lösning 7|1.1 Lösning 7}} | </div>{{#NAVCONTENT:Svar 7|1.1 Svar 7|Lösning 7|1.1 Lösning 7}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 7|Svar 7]] | [[1.1 Lösning 7|Lösning 7]]</small></small> | ||
| + | --> | ||
== Övning 8 == | == Övning 8 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande ekvation och ange svaret med två decimaler: | |
| + | |||
| + | <math> x\,\sqrt{x}\, + 4 = 8 </math> | ||
</div>{{#NAVCONTENT:Svar 8|1.1 Svar 8|Lösning 8|1.1 Lösning 8}} | </div>{{#NAVCONTENT:Svar 8|1.1 Svar 8|Lösning 8|1.1 Lösning 8}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 8|Svar 8]] | [[1.1 Lösning 8|Lösning 8]]</small></small> | ||
| + | --> | ||
| + | |||
| + | == A-övningar: 9-13 == | ||
== Övning 9 == | == Övning 9 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande rotekvation exakt: | |
| − | < | + | <math> 2 = - { x \over \sqrt{1-x^2} } </math> |
| − | + | </div>{{#NAVCONTENT:Svar 9|1.1 Svar 9|Lösning 9|1.1 Lösning 9}} | |
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 9|Svar 9]] | [[1.1 Lösning 9|Lösning 9]]</small></small> | ||
| + | --> | ||
== Övning 10 == | == Övning 10 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande ekvation exakt genom att använda en lämplig substitution: | |
| + | |||
| + | <math> {1 \over x} = 306 - {1 \over \sqrt{x}} </math> | ||
</div>{{#NAVCONTENT:Svar 10|1.1 Svar 10|Lösning 10|1.1 Lösning 10}} | </div>{{#NAVCONTENT:Svar 10|1.1 Svar 10|Lösning 10|1.1 Lösning 10}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 10|Svar 10]] | [[1.1 Lösning 10|Lösning 10]]</small></small> | ||
| + | --> | ||
== Övning 11 == | == Övning 11 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | + | Lös följande 4:e gradsekvation med en lämplig substitution: | |
| + | |||
| + | <math> {1\over2}\,(x^2 + 4\,x + 1)^2 = {3\over2}\,-\,(x^2 + 4\,x + 1) </math> | ||
</div>{{#NAVCONTENT:Svar 11|1.1 Svar 11|Lösning 11|1.1 Lösning 11}} | </div>{{#NAVCONTENT:Svar 11|1.1 Svar 11|Lösning 11|1.1 Lösning 11}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 11|Svar 11]] | [[1.1 Lösning 11|Lösning 11]]</small></small> | ||
| + | --> | ||
| + | |||
| + | == Övning 12 == | ||
| + | <div class="ovning"> | ||
| + | Lös ekvationen | ||
| + | |||
| + | <math> \sqrt{ x + 2 + \sqrt{2\;x + 7}} = 4 </math> | ||
| + | |||
| + | <!-- </div>{{#NAVCONTENT:Svar 12|1.1 Svar 12|Lösning 12|1.1 Lösning 12}} | ||
| + | Alternativt: | ||
| + | :<small><small>[[1.1 Svar 12|Svar 12]] | [[1.1 Lösning 12|Lösning 12]]</small></small> | ||
| + | --> | ||
| + | |||
| + | == Övning 13 == | ||
| + | <div class="ovning"> | ||
| + | Undersök om följande ekvation har en lösning. Om ja ange den. Om nej motivera: | ||
| + | |||
| + | <math> 6\;x = 1 - \sqrt{ 36\;x^2 - {1 \over x} } </math> | ||
| + | |||
| + | </div>{{#NAVCONTENT:Svar 13|1.1 Svar 13|Lösning 13|1.1 Lösning 13}} | ||
| + | <!-- Alternativt: | ||
| + | :<small><small>[[1.1 Svar 13|Svar 13]] | [[1.1 Lösning 13|Lösning 13]]</small></small> | ||
| + | --> | ||
| + | |||
| + | = Facit = | ||
| + | |||
| + | == 1a) == | ||
| + | <math> \displaystyle 81 </math> | ||
| + | |||
| + | == 1b) == | ||
| + | Ekvationen saknar lösning. | ||
| + | |||
| + | == 1c) == | ||
| + | <math> x = 16\, </math> | ||
| + | |||
| + | == 2a) == | ||
| + | <math> x = 1\, </math> | ||
| + | |||
| + | == 2b) == | ||
| + | <math> x = 1\, </math> | ||
| + | |||
| + | == 2c) == | ||
| + | <math> x = 0\, </math> | ||
| + | |||
| + | == 3a) == | ||
| + | <math> x = 2\, </math> | ||
| + | |||
| + | == 3b) == | ||
| + | <math> x = 36\, </math> | ||
| + | |||
| + | == 3c) == | ||
| + | <math> x_1 = 64\, </math> | ||
| + | |||
| + | <math> x_2 = 1\, </math> | ||
| + | |||
| + | == 4a) == | ||
| + | Ekvationen saknar lösning. | ||
| + | |||
| + | == 4b) == | ||
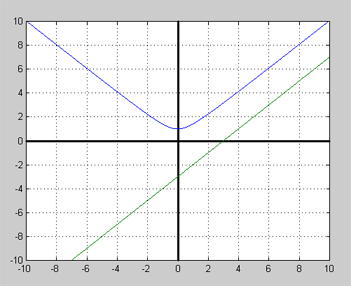
| + | Graferna till <math> y_1 = \sqrt{x^2 + 1} </math> och <math> \displaystyle y_2 = x - 3 </math> ritade i samma koordinatsystem: | ||
| + | |||
| + | [[Image: Rotekv_Övn_4bR.jpg]] | ||
| + | |||
| + | Bilden visar att kurvan <math> y_1 = \sqrt{x^2 + 1} </math> (blå) och linjen <math> \displaystyle y_2 = x - 3 </math> (grön) inte skär varandra. Dvs de har ingen gemensam punkt där deras funktionsvärden överensstämmer. | ||
| + | |||
| + | Detta bekräftar att ekvationen | ||
| + | |||
| + | <math> \sqrt{x^2 + 1} = x - 3 </math> | ||
| + | |||
| + | saknar lösning vilket visades i lösningen till [[1.1 Lösning 4a|övning 4a]]. | ||
| + | |||
| + | == 4c) == | ||
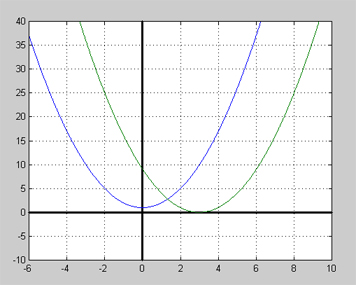
| + | Graferna till <math> \displaystyle y_1 = x^2 + 1 </math> och <math> \displaystyle y_2 = (x - 3)^2 </math> ritade i samma koordinatsystem: | ||
| + | |||
| + | [[Image: Rotekv_kvadrerad_Övn_4c.jpg]] | ||
| + | |||
| + | Bilden visar att kurvorna <math> \displaystyle y_1 = x^2 + 1 </math> (blå) och <math> \displaystyle y_2 = (x - 3)^2 </math> (grön) skär varandra i en punkt. Detta innebär att ekvationen | ||
| + | |||
| + | <math> \displaystyle x^2 + 1 = (x - 3)^2 </math> | ||
| + | |||
| + | har en lösning som kan avläsas från grafen till ca. <math> \displaystyle x \approx 1,3 </math>. Men denna ekvation uppstår när man kvadrerar den ursprungliga rotekvationen | ||
| + | |||
| + | <math> \sqrt{x^2 + 1} = x - 3 </math> | ||
| + | |||
| + | Dvs den kvadrerade ekvationen har en lösning som är den ursprungliga rotekvationens falska rot som är exakt <math> \displaystyle x = {4 \over 3} </math> vilket visades i lösningen till [[1.1 Lösning 4a|övning 4a]]. | ||
| + | |||
| + | == 5a) == | ||
| + | Den modifierade ekvationen är: | ||
| + | |||
| + | <math> \sqrt{x^2 + 1} = 3\,x - 3 </math> | ||
| + | |||
| + | == 5b) == | ||
| + | <math> x = 1,64\, </math> | ||
| + | |||
| + | == 6) == | ||
| + | Ekvationen | ||
| + | |||
| + | <math> x^4 - 29\;x^2 = -100 </math> | ||
| + | |||
| + | har lösningarna: | ||
| + | |||
| + | <math> x_1 = 5\, </math> | ||
| + | |||
| + | <math> x_2 = -5\, </math> | ||
| + | |||
| + | <math> x_3 = 2\, </math> | ||
| + | |||
| + | <math> x_4 = -2\, </math> | ||
| + | |||
| + | == 7) == | ||
| + | <math> x = 1\, </math> | ||
| + | |||
| + | == 8) == | ||
| + | <math> x = 2,52\, </math> | ||
| + | |||
| + | == 9) == | ||
| + | <math> x = - \; { 2 \over \sqrt{5} } </math> | ||
| + | |||
| + | == 10) == | ||
| + | <math> x = {1 \over 289} </math> | ||
| + | |||
| + | == 11) == | ||
| + | <math> x_1\, = 0 </math> | ||
| + | |||
| + | <math> x_2\, = -4 </math> | ||
| + | |||
| + | <math> x_3\, = -2 </math> | ||
| + | |||
| + | == 12) == | ||
| + | <math> x = 9\, </math> | ||
| + | |||
| + | == 13) == | ||
| + | <math> x = -{1 \over 4} </math> | ||
| + | |||
| + | |||
| + | |||
| + | [[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved. | ||
Nuvarande version från 4 augusti 2014 kl. 15.56
| Teori | Övningar |
E-övningar: 1-3
Övning 1
Lös följande rotekvationer:
a) \( {\color{White} x} \sqrt{x} = 9 \)
b) \( {\color{White} x} \sqrt{x} = - 9 \)
c) \( {\color{White} x} 5 - \sqrt{x} = 1 \)
Övning 2
Lös följande ekvationer med den metod som förklaras i teoridelen.
a) \( {\color{White} x} 2 \,\cdot \, \sqrt{x} - x = 1 \)
b) \( {\color{White} x} x + \sqrt{5\,x - 1} = 3 \)
c) \( {\color{White} x} 6\,x - 3\,\sqrt{9+x} = -9 \)
Övning 3
Lös följande rotekvationer:
a) \( {\color{White} x} x = \sqrt{x+7} - 1 \)
b) \( {\color{White} x} {x + \sqrt{x} \over 7} \) \( = 6 \)
c) \( {\color{White} x} 2\,(x + 8) = 9\,\sqrt{4\,x} \)
C-övningar: 4-8
Övning 4
Lös rotekvationen
a) \( \sqrt{x^2 + 1} = x - 3 \)
b) Rita graferna till funktionerna \( y_1 = \sqrt{x^2 + 1} \) och \( y_2 = x - 3\, \) i ett och samma koordinatsystem. Använd följande inställningar för WINDOW i din grafritande räknare: Xmin = -10, Xmax = 10, Xscl = 2, Ymin = -10, Ymax = 10, Yscl = 2. Motivera ditt svar i a) med hjälp av graferna.
c) Rita graferna till funktionerna \( \displaystyle y_1 = x^2 + 1 \) och \( y_2 = (x - 3)^2\, \) i ett och samma koordinatsystem. Använd följande inställningar för WINDOW i din grafritande räknare: Xmin = -3, Xmax = 6, Xscl = 1, Ymin = 0, Ymax = 10, Yscl = 1. Tolka resultatet.
Övning 5
a) Modifiera rotekvationen
\( \sqrt{x^2 + 1} = x - 3 \)
i övning 4 så att den får en lösning genom att titta på grafen som du (förhoppningsvis) ritade i övning 4b. Rita graferna till funktionerna på bägge leden av den modifierade rotekvationen i ett och samma koordinatsystem så att man ser lösningen grafiskt. Använd samma inställningar för WINDOW i din grafritande räknare som i övning 4b.
b) Lös den modifierade rotekvationen algebraiskt. Ange svaret med 2 decimalers noggrannhet.
Övning 6
Lös ekvationen
\( x^4 - 29\;x^2 = -100 \)
Övning 7
Lös följande ekvation, som är samma som i övning 2a, här med substitutionen \( t = \sqrt{x} \).
\( 2\,\sqrt{x} - x = 1 \)
Övning 8
Lös följande ekvation och ange svaret med två decimaler\[ x\,\sqrt{x}\, + 4 = 8 \]
A-övningar: 9-13
Övning 9
Lös följande rotekvation exakt\[ 2 = - { x \over \sqrt{1-x^2} } \]
Övning 10
Lös följande ekvation exakt genom att använda en lämplig substitution\[ {1 \over x} = 306 - {1 \over \sqrt{x}} \]
Övning 11
Lös följande 4:e gradsekvation med en lämplig substitution\[ {1\over2}\,(x^2 + 4\,x + 1)^2 = {3\over2}\,-\,(x^2 + 4\,x + 1) \]
Övning 12
Lös ekvationen
\( \sqrt{ x + 2 + \sqrt{2\;x + 7}} = 4 \)
Övning 13
Undersök om följande ekvation har en lösning. Om ja ange den. Om nej motivera\[ 6\;x = 1 - \sqrt{ 36\;x^2 - {1 \over x} } \]
Facit
1a)
\( \displaystyle 81 \)
1b)
Ekvationen saknar lösning.
1c)
\( x = 16\, \)
2a)
\( x = 1\, \)
2b)
\( x = 1\, \)
2c)
\( x = 0\, \)
3a)
\( x = 2\, \)
3b)
\( x = 36\, \)
3c)
\( x_1 = 64\, \)
\( x_2 = 1\, \)
4a)
Ekvationen saknar lösning.
4b)
Graferna till \( y_1 = \sqrt{x^2 + 1} \) och \( \displaystyle y_2 = x - 3 \) ritade i samma koordinatsystem:
Bilden visar att kurvan \( y_1 = \sqrt{x^2 + 1} \) (blå) och linjen \( \displaystyle y_2 = x - 3 \) (grön) inte skär varandra. Dvs de har ingen gemensam punkt där deras funktionsvärden överensstämmer.
Detta bekräftar att ekvationen
\( \sqrt{x^2 + 1} = x - 3 \)
saknar lösning vilket visades i lösningen till övning 4a.
4c)
Graferna till \( \displaystyle y_1 = x^2 + 1 \) och \( \displaystyle y_2 = (x - 3)^2 \) ritade i samma koordinatsystem:
Bilden visar att kurvorna \( \displaystyle y_1 = x^2 + 1 \) (blå) och \( \displaystyle y_2 = (x - 3)^2 \) (grön) skär varandra i en punkt. Detta innebär att ekvationen
\( \displaystyle x^2 + 1 = (x - 3)^2 \)
har en lösning som kan avläsas från grafen till ca. \( \displaystyle x \approx 1,3 \). Men denna ekvation uppstår när man kvadrerar den ursprungliga rotekvationen
\( \sqrt{x^2 + 1} = x - 3 \)
Dvs den kvadrerade ekvationen har en lösning som är den ursprungliga rotekvationens falska rot som är exakt \( \displaystyle x = {4 \over 3} \) vilket visades i lösningen till övning 4a.
5a)
Den modifierade ekvationen är\[ \sqrt{x^2 + 1} = 3\,x - 3 \]
5b)
\( x = 1,64\, \)
6)
Ekvationen
\( x^4 - 29\;x^2 = -100 \)
har lösningarna\[ x_1 = 5\, \]
\( x_2 = -5\, \)
\( x_3 = 2\, \)
\( x_4 = -2\, \)
7)
\( x = 1\, \)
8)
\( x = 2,52\, \)
9)
\( x = - \; { 2 \over \sqrt{5} } \)
10)
\( x = {1 \over 289} \)
11)
\( x_1\, = 0 \)
\( x_2\, = -4 \)
\( x_3\, = -2 \)
12)
\( x = 9\, \)
13)
\( x = -{1 \over 4} \)
 Hämtar...
Hämtar...