Skillnad mellan versioner av "2.1 Mängd, element och delmängd"

Från Mathonline
Hoppa till: navigering, sök
(Skapade sidan med '__NOTOC__ {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" |   {{Not selected tab|1.10 Indir...')
 
m
 
(52 mellanliggande versioner av samma användare visas inte)
Rad 3: Rad 3:
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
{{Not selected tab|[[1.10 Indirekta bevis|<<&nbsp;&nbsp;Förra avsnitt]]}}
 
{{Not selected tab|[[1.10 Indirekta bevis|<<&nbsp;&nbsp;Förra avsnitt]]}}
 +
{{Not selected tab|[[Matte 5 Innehållsförteckning|Innehållsförteckning]]}}
 
{{Selected tab|[[2.1 Mängd, element och delmängd|Genomgång]]}}
 
{{Selected tab|[[2.1 Mängd, element och delmängd|Genomgång]]}}
−
{{Not selected tab|[[Matte 5 Innehållsförteckning|Innehållsförteckning]]}}
+
<!-- {{Not selected tab|[https://sharedfiles.mathonline.se/Planering_Matte_5_ht_24.pdf Planering]}} -->
−
{{Not selected tab|[https://sharedfiles.mathonline.se/Planering_Matte_5_ht_24.pdf Planering]}}
+
 
{{Not selected tab|[[2.1 Övningar till Mängd, element och delmängd|Övningar]]}}
 
{{Not selected tab|[[2.1 Övningar till Mängd, element och delmängd|Övningar]]}}
 +
{{Not selected tab|[[2.2 Mängdoperationer och deras logik|Nästa avssnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
= <b><span style="color:#931136">Vad handlar kombinatorik om?</span></b> =
+
= <b><span style="color:#931136">Mängd och element</span></b> =
 
<div class="ovnE">
 
<div class="ovnE">
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Dirichlet_Ladprincip_1.jpg]] </div>
+
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Mangd_Element.jpg]] </div>
−
 
+
−
 
+
−
<big>Ett liknande exempel är brevbärarens placering av ett antal brev (föremål) i ett antal brevlådor.</big>
+
−
 
+
−
 
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Dirichlet_Ladprincip_2.jpg]] </div>
+
 
</div>
 
</div>
  
  
−
<div class="border-divblue">
+
<div class="ovnC">
−
<big><b>Om vi stryker ordet "endast" (ovan), dvs om det även kan gå flera pilar från A,
+
<table>
−
 
+
<tr>
−
har vi en <span style="color:red">relation</span> mellan A och B. En annan tolkning är en <span style="color:red">avbildning</span> från A till B.
+
<td><big><big><b><span style="color:#931136">Delmängd</span></b></big></big>
−
 
+
<br>
−
En relation är en delmängd av den Cartesiska produkten <math> A \times B </math> .</b></big>
+
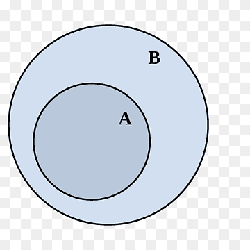
<big>A är en delmängd till B: <br><br> <math> \qquad\quad A \subset B </math> <br><br>
 +
om: <br><br> x ∈ A ⇒ x ∈ B, för alla x.</big>
 +
</td>
 +
<td> <math> \qquad </math> </td>
 +
<td> <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Delmangd_250a.png]] </div>  
 +
</td>
 +
</tr>
 +
</table>
 
</div>
 
</div>
  
  
−
= <b><span style="color:#931136">Uppgift</span></b> =
+
= <b><span style="color:#931136">Exempel på delmängder</span></b> =
−
<div class="ovnC">
+
<div class="ovnA">
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: Dirichlet_Ovn_Losg.jpg]] </div>
+
<big><big>
 +
<math> \qquad\;\; </math><div class="smallBox">[https://matte1b.mathonline.se/index.php?title=1.1_Om_tal#Olika_typer_av_tal <b><span style="color:blue">Olika typer av tal</span></b>]</div><math> \qquad\;\;\, </math>
 +
</big></big>
 
</div>
 
</div>
  
  
−
 
+
<br>
  
  

Nuvarande version från 3 november 2024 kl. 12.06

       <<  Förra avsnitt          Innehållsförteckning          Genomgång          Övningar          Nästa avssnitt  >>      


Mängd och element

Mangd Element.jpg


Delmängd


A är en delmängd till B:

\( \qquad\quad A \subset B \)

om:

x ∈ A ⇒ x ∈ B, för alla x.

\( \qquad \)
Delmangd 250a.png


Exempel på delmängder

\( \qquad\;\; \)
Olika typer av tal
\( \qquad\;\;\, \)







Copyright © 2024 Lieta AB. All Rights Reserved.

Hämtad från "https://matte5.mathonline.se/index.php?title=2.1_Mängd,_element_och_delmängd&oldid=23794"