Skillnad mellan versioner av "1.2 Övningar till Faktorisering av polynom"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (12 mellanliggande versioner av samma användare visas inte) | |||
| Rad 2: | Rad 2: | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[1.2 Repetition Faktorisering & Vieta från Matte 2|Repetition: Faktorisering]]}} | + | {{Not selected tab|[[1.2 Repetition Faktorisering & Vieta från Matte 2|Repetition: Faktorisering & Vieta]]}} |
| − | {{Not selected tab|[[1.2 Faktorisering av polynom| | + | {{Not selected tab|[[1.2 Faktorisering av polynom|Genomgång]]}} |
{{Selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}} | {{Selected tab|[[1.2 Övningar till Faktorisering av polynom|Övningar]]}} | ||
{{Not selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}} | {{Not selected tab|[[1.2 Fördjupning till Faktorisering av Polynom|Fördjupning]]}} | ||
| Rad 95: | Rad 95: | ||
c) <math> {\color{White} x} 4\,x^2 - 36 </math> | c) <math> {\color{White} x} 4\,x^2 - 36 </math> | ||
| − | </div>{{#NAVCONTENT:Svar 6a|1.3 Svar 6a|Lösning 6a|1. | + | </div>{{#NAVCONTENT:Svar 6a|1.3 Svar 6a|Lösning 6a|1.2 Lösning 6a|Svar 6b|1.3 Svar 6b|Lösning 6b|1.3 Lösning 6b|Svar 6c|1.3 Svar 6c|Lösning 6c|1.3 Lösning 6c}} |
<!-- Alternativt: | <!-- Alternativt: | ||
:<small><small>[[1.3 Svar 6a|Svar 6a]] | [[1.3 Lösning 6a|Lösning 6a]] | [[1.3 Svar 6b|Svar 6b]] | [[1.3 Lösning 6b|Lösning 6b]] | [[1.3 Svar 6c|Svar 6c]] | [[1.3 Lösning 6c|Lösning 6c]]</small></small> | :<small><small>[[1.3 Svar 6a|Svar 6a]] | [[1.3 Lösning 6a|Lösning 6a]] | [[1.3 Svar 6b|Svar 6b]] | [[1.3 Lösning 6b|Lösning 6b]] | [[1.3 Svar 6c|Svar 6c]] | [[1.3 Lösning 6c|Lösning 6c]]</small></small> | ||
| Rad 169: | Rad 169: | ||
Följande 4:e gradspolynom är givet och har dubbelroten <math> x = -1\,</math>: | Följande 4:e gradspolynom är givet och har dubbelroten <math> x = -1\,</math>: | ||
| − | :<math> P(x) = x^4 - 7\,x^3 + 3\,x^2 + 31\,x + 20 </math> | + | ::<math> P(x) = x^4 - 7\,x^3 + 3\,x^2 + 31\,x + 20 </math> |
a) Ange med hjälp av dubbelroten en delfaktorisering av <math> P(x)\,</math>. | a) Ange med hjälp av dubbelroten en delfaktorisering av <math> P(x)\,</math>. | ||
| Rad 182: | Rad 182: | ||
== Övning 12 == | == Övning 12 == | ||
<div class="ovning"> | <div class="ovning"> | ||
| − | Anta att | + | Anta att polynomet |
| − | :<math> P(x) = x^4 + 3\,x^3 - 7\,x^2 - 27\,x - 18 </math> | + | ::<math> P(x) = x^4 + 3\,x^3 - 7\,x^2 - 27\,x - 18 </math> |
| − | har | + | har två nollställen <math> a\,</math> och <math> -a\,</math>. |
a) Bestäm dessa två nollställen och ange en delfaktorisering av <math> P(x)\,</math>. | a) Bestäm dessa två nollställen och ange en delfaktorisering av <math> P(x)\,</math>. | ||
| Rad 206: | Rad 206: | ||
:::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math> | :::::<math> x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) </math> | ||
| − | <b>Ledning:</b> Sätt in p-q-formeln för <math> x_1\, </math> och <math> x_2\, </math> i högerledet och utveckla produkten | + | <b>Ledning:</b> Sätt in p-q-formeln för <math> x_1\, </math> och <math> x_2\, </math> i högerledet och utveckla produkten för att visa likheten med vänsterledet. |
| − | + | ||
| − | + | ||
</div>{{#NAVCONTENT:Lösning 13|1.2 Lösning 13}} | </div>{{#NAVCONTENT:Lösning 13|1.2 Lösning 13}} | ||
| Rad 224: | Rad 222: | ||
a) Börja med en delfaktorisering inom ramen av de reella talen. | a) Börja med en delfaktorisering inom ramen av de reella talen. | ||
| − | b) Fortsätt sedan | + | b) Fortsätt sedan med fullständig faktorisering till linjära faktorer genom att hitta även <math> \, P(x)</math>:s komplexa rötter. |
| − | + | ||
| − | + | ||
| − | + | ||
| + | </div>{{#NAVCONTENT:Ledning 14|1.2 Lösning 14|Lösning 12|1.2 Lösninga 14}} | ||
| + | <!-- | ||
<Big><Big><Big><span style="color:blue"><u>Facit</u></span></Big></Big></Big> | <Big><Big><Big><span style="color:blue"><u>Facit</u></span></Big></Big></Big> | ||
| − | |||
== 1) == | == 1) == | ||
| Rad 313: | Rad 309: | ||
== 12b) == | == 12b) == | ||
<math> (x+3) \cdot (x-3) \cdot (x+1) \cdot (x+2) </math> | <math> (x+3) \cdot (x-3) \cdot (x+1) \cdot (x+2) </math> | ||
| − | + | --> | |
| + | |||
| + | |||
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved. | [[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved. | ||
Nuvarande version från 14 maj 2015 kl. 21.40
| Repetition: Faktorisering & Vieta | Genomgång | Övningar | Fördjupning | Nästa avsnitt --> |
E-övningar: 1-6
Övning 1
Om
- \[ x^3 - 5\,x^2 + 12\,x - 6 = (x-2) \cdot {\rm (ett\ polynom)} \]
vad är då graden till det okända polynomet?
Övning 2
Vi har:
- \[ 4\,x^2 + 16\,x - 8 = (x+3) \cdot {\rm (ett\ polynom)} \]
a) Vad är graden till det okända polynomet?
b) Vad är koefficienten till x-termen i det okända polynomet?
Övning 3
Ange ett polynom i faktorform vars nollställen är:
a) \( {\color{White} x} 2 \, \) och \( 6 \, \)
b) \( {\color{White} x} -2 \, \) och \( -6 \, \)
c) \( {\color{White} x} 1 \, \), och \( -5 \, \) och \( 4 \, \)
Övning 4
Ange nollställen till följande polynom:
a) \( {\color{White} x} (x-2) \cdot (x+1) \)
b) \( {\color{White} x} (3\,x-1) \cdot (2\,x+1) \)
Övning 5
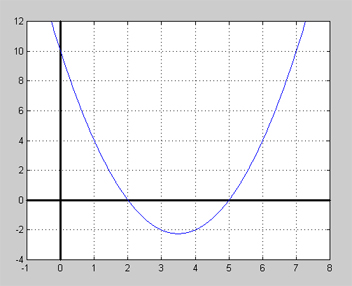
Grafen till en polynomfunktion ser ut så här:
a) Ange några exempel på polynom i faktorform vars nollställen är identiska med kurvans nollställen.
b) Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 6
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten:
a) \( {\color{White} x} x^2 - 6\,x + 8 \)
b) \( {\color{White} x} 3\,x^2 + 3\,x - 6 \)
c) \( {\color{White} x} 4\,x^2 - 36 \)
C-övningar: 7-10
Övning 7
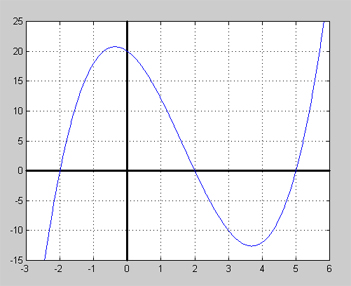
Grafen till en polynomfunktion ser ut så här:
Ange det polynom i faktorform vars graf är kurvan ovan.
Övning 8
Faktorisera följande polynom och kontrollera dina svar genom utveckling av de erhållna resultaten. Ange slutresultaten med heltalskoefficienter.
a) \( {\color{White} x} 9\,x^2 - 6\,x + 1 \)
b) \( {\color{White} x} x^2 + 4\,x + 5 \)
c) \( {\color{White} x} 49\,z^2 + 14\,z + 1 \)
Övning 9
Ange den fullständiga faktoriseringen av polynomet
- \[ x^3 - 9\,x^2 + 26\,x - 24 \]
om en av faktorerna är \( (x-4)\, \).
Övning 10
Vi har följande delfaktorisering av ett 3:e gradspolynom:
- \[ x^3 - 17\,x^2 + 54\,x - 8 = (x-4) \cdot {\rm (ett\ polynom)} \]
a) Bestäm det okända polynomet som en summa av termer.
b) Ange 3:e gradspolynomets fullständiga faktorisering. Svara med två decimaler.
A-övningar: 11-14
Övning 11
Följande 4:e gradspolynom är givet och har dubbelroten \( x = -1\,\):
- \[ P(x) = x^4 - 7\,x^3 + 3\,x^2 + 31\,x + 20 \]
a) Ange med hjälp av dubbelroten en delfaktorisering av \( P(x)\,\).
b) Faktorisera \( P(x)\,\) fullständigt.
Övning 12
Anta att polynomet
- \[ P(x) = x^4 + 3\,x^3 - 7\,x^2 - 27\,x - 18 \]
har två nollställen \( a\,\) och \( -a\,\).
a) Bestäm dessa två nollställen och ange en delfaktorisering av \( P(x)\,\).
b) Faktorisera \( P(x)\,\) fullständigt.
Övning 13
Bevisa satsen om faktorisering med 2 nollställen:
Sats: Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:
- \[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]
Ledning: Sätt in p-q-formeln för \( x_1\, \) och \( x_2\, \) i högerledet och utveckla produkten för att visa likheten med vänsterledet.
Övning 14
Faktorisera fullständigt 5:e gradspolynomet \( P(x)\, \):
- \[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 \]
a) Börja med en delfaktorisering inom ramen av de reella talen.
b) Fortsätt sedan med fullständig faktorisering till linjära faktorer genom att hitta även \( \, P(x)\):s komplexa rötter.
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.
 Hämtar...
Hämtar...