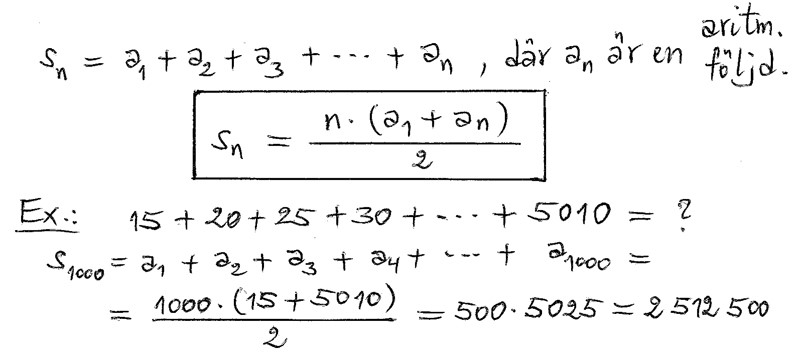Skillnad mellan versioner av "1.6 Aritmetisk summa och summatecknet"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 36: | Rad 36: | ||
Eller istället för att skriva den långa summan <math>1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20</math> | Eller istället för att skriva den långa summan <math>1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20</math> | ||
| − | kan man | + | kan man skriva <math> \qquad \sum_{k=1}^{20} k = 1 + 2 + 3 + \ldots + 19 + 20</math>. |
| − | : | + | Detta läses: "Summa ''k'', då ''k'' går från ett till tjugo". ''k'' kallas '''summand'''. |
| − | + | Vill man skriva summan av alla [[heltal]] från och med 7 till och med 23 skriver man<span>:</span> | |
| − | + | ||
| − | Vill man skriva summan av alla [[heltal]] från och med 7 till och med 23 skriver man: | + | |
| − | : <math>\sum_{k=7}^{23} k = 7 + 8 + 9 + \ldots + 22 + 23</math> | + | ::::<math>\sum_{k=7}^{23} k = 7 + 8 + 9 + \ldots + 22 + 23</math> |
| − | Vill man summera t.ex. kvadraterna av alla tal från 1 till 5 skriver man: | + | Vill man summera t.ex. kvadraterna av alla tal från 1 till 5 skriver man<span>:</span> |
| − | : <math>\sum_{k=1}^5 k^2 = 1 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55</math> | + | ::::<math>\sum_{k=1}^5 k^2 = 1 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55</math> |
</big> | </big> | ||
</div> | </div> | ||
Versionen från 29 juni 2024 kl. 18.40
| << Förra avsnitt | Innehållsförteckning | Genomgång | Övningar | Nästa avsnitt >> |
Aritmetisk summa = Summan av en aritmetisk talföljd
Summatecknet \( \; \sum \; \)
Den stora bokstaven Sigma i det grekiska alfabetet används i matematiken som symbol för summa.
Man gör det för att kunna skriva långa summor på ett kompakt sätt.
Rutan ovan skulle \(-\) skriven med summatecknet \(-\) inledas så här:
\( \quad s_n \, = \, \displaystyle\sum_{k=1}^{n} a_k \; \), där \( \; a_n \; \) är en aritmetisk följd. \( \quad \)
Eller istället för att skriva den långa summan \(1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20\)
kan man skriva \( \qquad \sum_{k=1}^{20} k = 1 + 2 + 3 + \ldots + 19 + 20\).
Detta läses: "Summa k, då k går från ett till tjugo". k kallas summand.
Vill man skriva summan av alla heltal från och med 7 till och med 23 skriver man:
- \[\sum_{k=7}^{23} k = 7 + 8 + 9 + \ldots + 22 + 23\]
Vill man summera t.ex. kvadraterna av alla tal från 1 till 5 skriver man:
- \[\sum_{k=1}^5 k^2 = 1 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55\]
Copyright © 2024 Lieta AB. All Rights Reserved.