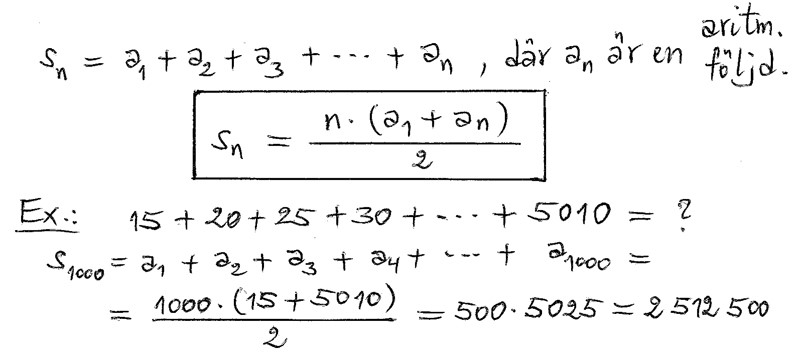Skillnad mellan versioner av "1.6 Aritmetisk summa och summatecknet"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 22: | Rad 22: | ||
Den stora bokstaven <span style="color:red">Sigma</span> i det grekiska alfabetet används i matematiken som symbol för <span style="color:red">summa</span>. | Den stora bokstaven <span style="color:red">Sigma</span> i det grekiska alfabetet används i matematiken som symbol för <span style="color:red">summa</span>. | ||
| + | Man gör det för att kunna skriva långa summor på ett kompakt sätt. | ||
Om ett större antal termer ska adderas, kan summan skrivas med hjälp av summasymbolen Σ; den stora bokstaven [[sigma]] i det grekiska alfabetet. [[Jean-Baptiste Joseph Fourier|Joseph Fourier]] införde sigma som symbol för summation 1820.<ref>Concrete Mathematics, sid. 22</ref> Istället för att skriva det långa talet <math>1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20</math> kan man använda summasymbolen samman med [[uteslutningstecken]] (<math>\ldots</math>) och skriva: | Om ett större antal termer ska adderas, kan summan skrivas med hjälp av summasymbolen Σ; den stora bokstaven [[sigma]] i det grekiska alfabetet. [[Jean-Baptiste Joseph Fourier|Joseph Fourier]] införde sigma som symbol för summation 1820.<ref>Concrete Mathematics, sid. 22</ref> Istället för att skriva det långa talet <math>1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20</math> kan man använda summasymbolen samman med [[uteslutningstecken]] (<math>\ldots</math>) och skriva: | ||
Versionen från 29 juni 2024 kl. 16.37
| << Förra avsnitt | Innehållsförteckning | Genomgång | Övningar | Nästa avsnitt >> |
Aritmetisk summa = Summan av en aritmetisk talföljd
Summatecknet \( \; \sum \; \)
Den stora bokstaven Sigma i det grekiska alfabetet används i matematiken som symbol för summa.
Man gör det för att kunna skriva långa summor på ett kompakt sätt.
Om ett större antal termer ska adderas, kan summan skrivas med hjälp av summasymbolen Σ; den stora bokstaven sigma i det grekiska alfabetet. Joseph Fourier införde sigma som symbol för summation 1820.<ref>Concrete Mathematics, sid. 22</ref> Istället för att skriva det långa talet \(1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20\) kan man använda summasymbolen samman med uteslutningstecken (\(\ldots\)) och skriva: \[\sum_{k=1}^{20} k = 1 + 2 + 3 + \ldots + 19 + 20\] Detta utläses: "Summa k, då k går från ett till tjugo". Termen k efter sigmatecknet kallas summand. Vill man skriva summan av alla heltal från och med 7 till och med 23 skriver man: \[\sum_{k=7}^{23} k = 7 + 8 + 9 + \ldots + 22 + 23\] Vill man summera kvadraterna av alla tal från 1 till 5 skriver man: \[\sum_{k=1}^5 k^2 = 1 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55\] Ibland skrivs summationsgränserna vid sidan av summatecknet för att spara plats, exempelvis i bråk: \[\frac{\sum_{k=1}^{20} k^2}{\sum_{j=1}^{20} j^3}\]
Allmänt, givet en talföljd \(a_k\) som man vill summera från 1 till n skriver man: \[\sum_{k=1}^n a_k\,\] Summan ovan kan även skrivas \[\sum_{1 \leq k \leq n} a_k\,\] Rent allmänt används summatecknet för att summera en följd av tal \(a_k\) där k ska uppfylla något villkor \(P(k)\), vilket skrivs \[\sum_{P(k)} a_k\,\] Exempelvis kan \(P(k)\) vara villkoret att k är ett primtal eller ett udda tal.
Copyright © 2024 Lieta AB. All Rights Reserved.